Example F.11C – Single-Angle Flexural Member with Vertical and Horizontal Loading

This benchmark reproduces the calculations and evaluation process from Example F.11C – Single-Angle Flexural Member with Vertical and Horizontal Loading in the AISC Design Examples manual. Using SDC Verifier 2025 R1, we model the same geometry, loading conditions, and material assumptions to verify alignment between automated results and the manual benchmark.

The study includes uniform vertical dead and live loads along with a horizontal wind load, acting on a simply supported angle braced only at the ends. Both LRFD and ASD design methodologies are evaluated according to ASCE/SEI 7 load combinations, with the material defined as ASTM A36.

This benchmark serves to:

• Validate SDC Verifier’s limit state checks against AISC manual results.

• Highlight differences due to FEA modeling simplifications (e.g. fillet radii).

• Confirm governing flexural limit states across both major and minor principal axes.

Task

Directly applying the requirements of the AISC Specification, select a single angle for span and uniform vertical dead and live loads as shown in Figure F.11C-1. The horizontal load is a uniform wind load. There is no deflection limit for this angle. The angle is simply supported and braced at the end points only and there is no lateral-torsional restraint.

Use:

• Load combination 4 from Section 2.3.1 of ASCE/SEI 7 for LRFD
• Load combination 6 from Section 2.4.1 of ASCE/SEI 7 for ASD

The angle is ASTM A36 material.

---

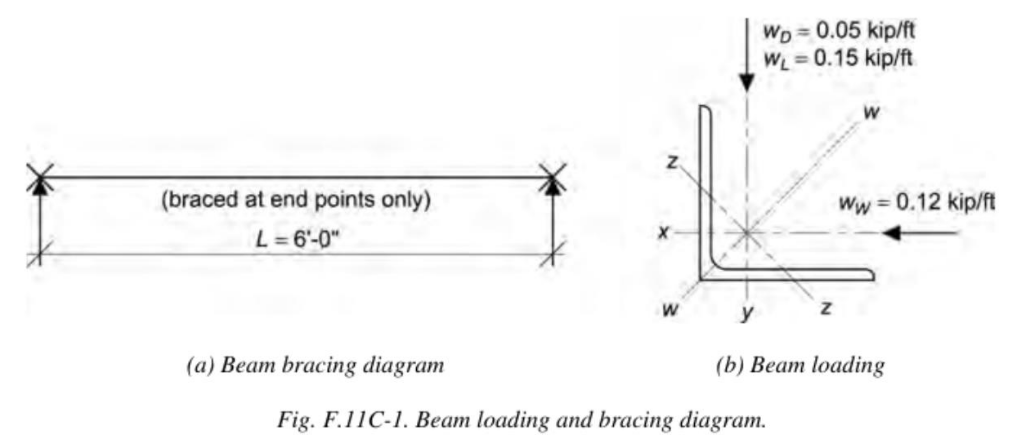
Loading and Bracing Diagram (Fig. F.11C-1)

(a) Beam Bracing Diagram:

• Braced at end points only
• Span: (L = 6′ – 0″)

(b) Beam Loading:

• Dead Load: ( w_D = 0.05, kip/ft (vertical)
• Live Load: ( w_L = 0.15, kip/ft (vertical)
• Wind Load: ( w_W = 0.12, kip/ft (horizontal)

Solution

From AISC Manual Table 2-4, the material properties are:

• ASTM A36
  F_y = 36, ksi
  F_u = 58, ksi

---

From Chapter 2 of ASCE/SEI 7, the required flexural strength is:

Try a L4×4×¼.

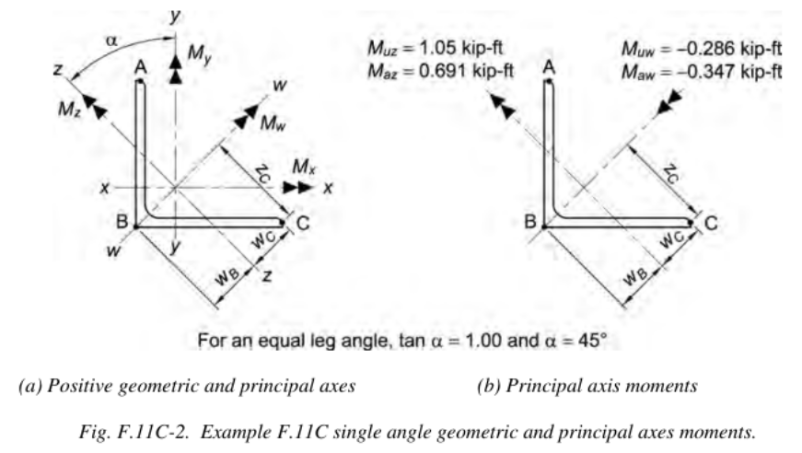
Sign Convention for Geometric Axes Moments

Principal Axes Moments (from Figure F.11C-2)

Geometric Properties (From AISC Manual Table 1-7)

L4×4×¼

A = 1.93 in.²

S_x = S_y = 1.03 in.³

I_x = I_y = 3.00 in.⁴

I_z = 1.19 in.⁴

r_z = 0.783 in.

Principal Axes Properties (From AISC Shapes Database)

w_B = 1.53 in.

w_C = 1.39 in.

z_C = 2.74 in.

I_w = 4.82 in.⁴

S_B = 0.778 in.³

S_C = 0.856 in.³

S_wC = 1.76 in.³

Z-Axis Nominal Flexural Strength

Note:
M_uz and M_az are positive; therefore, the toes of the angle are in compression.

---

Flexural Yielding

From AISC Specification Section F10.1, the nominal flexural strength due to the limit state of flexural yielding is:

M_nz = 1.5 M_y (from Spec. Eq. F10-1)

= 1.5 F_y S_zB

= 1.5 × (36 ksi) × (0.778 in.³)

= 42.0 kip-in.

Lateral-Torsional Buckling

From the User Note in AISC Specification Section F10:

The limit state of lateral-torsional buckling does not apply for bending about the minor axis.

---

Leg Local Buckling

Check slenderness of the outstanding leg in compression:

λ = b / t

= 4.00 in. / ¼ in.

= 16.0

Limiting Width-to-Thickness Ratios

From AISC Specification Table B4.1b, Case 12:

λ_p = 0.54 √(E / F_y)

= 0.54 √(29,000 ksi / 36 ksi)

= 15.3

λ_r = 0.91 √(E / F_y)

= 0.91 √(29,000 ksi / 36 ksi)

= 25.8

Flexural Yielding (Noncompact Leg)

Because
λ_p < λ < λ_r,
the leg is noncompact in flexure.

S_c = S_zC (to toe in compression)

= 0.856 in.³

M_nz = F_y S_c [2.43 – 1.72 (b/t) √(F_y/E)] (Spec. Eq. F10-6)

= (36 ksi)(0.856 in.³) × [2.43 – 1.72(16.0) √(36 ksi / 29,000 ksi)]

= 45.0 kip-in.

Flexural Yielding Limit State Controls

M_nz = 42.0 kip-in. or 3.50 kip-ft

Z-Axis Available Flexural Strength

From AISC Specification Section F1:

W-Axis Nominal Flexural Strength

Flexural Yielding

(from Spec. Eq. F10-1)

M_nw = 1.5 M_y

= 1.5 F_y S_wC

= 1.5 × (36 ksi) × (1.76 in.³)

= 95.0 kip-in.

Lateral-Torsional Buckling

Determine M_cr

For bending about the major principal axis of an equal-leg angle without continuous lateral-torsional restraint, use:

AISC Specification Equation F10-4
C_b = 1.14 from Manual Table 3-1
β_w = 0 (from AISC Specification Section F10.2(b)(1), for equal leg angles)

Critical Moment M_cr:

M_cr = [9 E A r_z t C_b] / [8 L_b] × √{1 + 4.4 (β_w r_z / L_bf)² + 4.4 (β_w r_z / L_bf)}

= 9 × (29,000 ksi) × (1.93 in.²) × (0.783 in.) × (¼ in.) × (1.14)

÷ [8 × (6 ft) × (12 in./ft)]

× √{1 + 4.4 × [0 × (0.783 in.) / ((6 ft)(12 in./ft)(¼ in.))]² + 4.4 × [0 × (0.783 in.) / ((6 ft)(12 in./ft)(¼ in.))]}

= 195 kip-in.

Yielding Moment for Comparison

M_y = F_y S_wC

= (36 ksi) × (1.76 in.³)

= 63.4 kip-in.

M_y / M_cr = 63.4 kip-in. / 195 kip-in.

= 0.325 < 1.0, therefore AISC Specification Equation F10-2 is applicable

M_nw = [1.92 – 1.17 √(M_y / M_cr)] × M_y ≤ 1.5 M_y (Spec. Eq. F10-2)

= [1.92 – 1.17 √(63.4 / 195)] × (63.4 kip-in.)

≤ 1.5 × (63.4 kip-in.) = 95.1 kip-in.

= 79.4 kip-in. < 95.1 kip-in.

= 79.4 kip-in.

Leg Local Buckling

From the preceding calculations, the leg is noncompact in flexure

S_c = S_wC (to toe in compression)

= 1.76 in.³

M_nw = F_y S_c × [2.43 – 1.72 (b/t) √(F_y / E)] (Spec. Eq. F10-6)

= (36 ksi)(1.76 in.³) × [2.43 – 1.72(16.0) √(36 ksi / 29,000 ksi)]

= 92.5 kip-in.

Lateral-Torsional Buckling Limit State Controls

M_nw = 79.4 kip-in. or 6.62 kip-ft

W-Axis Available Flexural Strength

From AISC Specification Section F1:

Combined Loading

The moment resultant has components about both principal axes; therefore, the combined stress ratio must be checked using the provisions of AISC Specification Section H2:

| f_ra / F_ca + f_rbw / F_cbw + f_rbz / F_cbz | ≤ 1.0 (Spec. Eq. H2-1)

Note:
Rather than convert moments into stresses, it is acceptable to simply use the moments in the interaction equation. The section properties cancel out, so the numerator and denominator match. It’s important to track the signs of the stresses to ensure proper application. Signs help determine tension/compression, but aren’t used directly in the interaction ratios.

Summary of Required vs. Available Flexural Strength

(Based on Figure F.11C-2)

Stress Checks at Critical Points

At point B:

M_w causes no stress, so the stress ratio is 0. M_z causes tension → taken as negative.

At point C:

M_w causes tension → negative; M_z causes compression → positive.

At point A:

M_w and M_z both cause compression → positive.

Thus, the interaction of stresses at each point is seen to be less than 1.0 and this member is adequate to carry the required load.
Although all three points were checked, it was expected that point A would be the controlling point, because compressive stresses add at this point.

Example from AISC Design Examples 

Material Summary 

Properties Summary 

Some slight differences in geometrical properties may be noticed, but these come from the fact that the cross-section is modeled without a root fillet radius and toe radius due to FEA simplifications.

FEM Loads and Constraints 

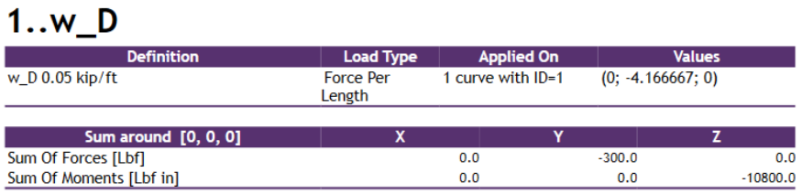
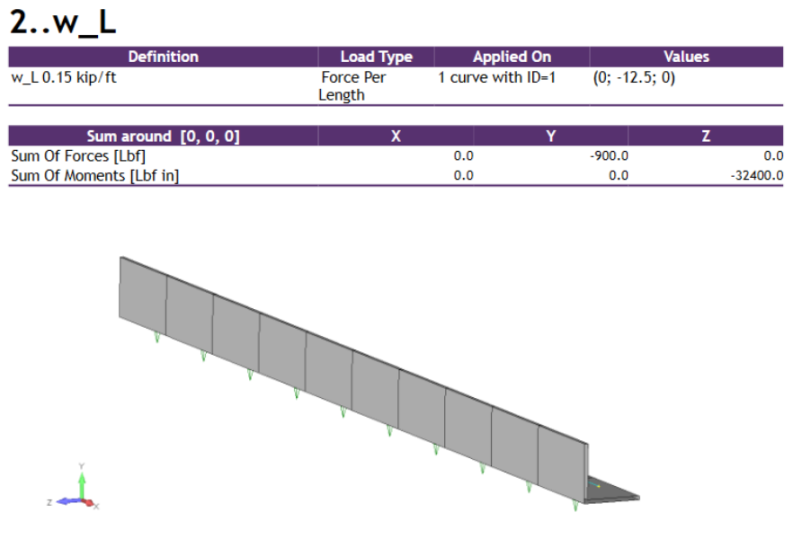
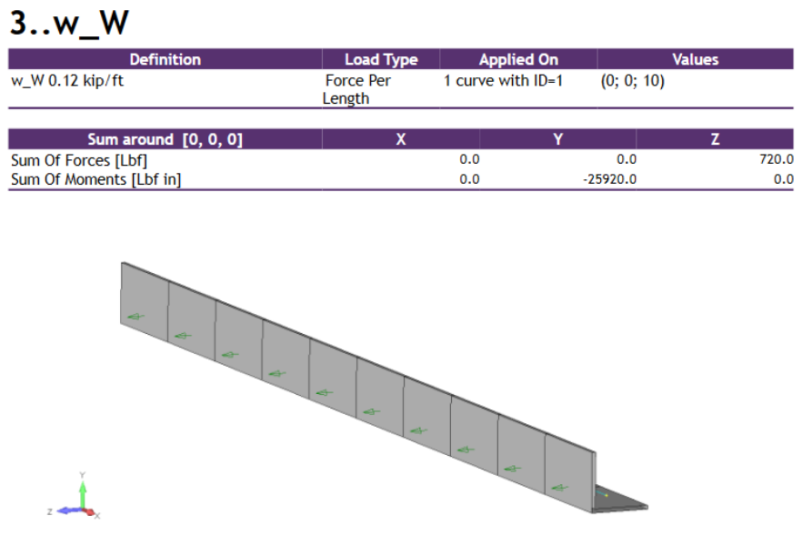
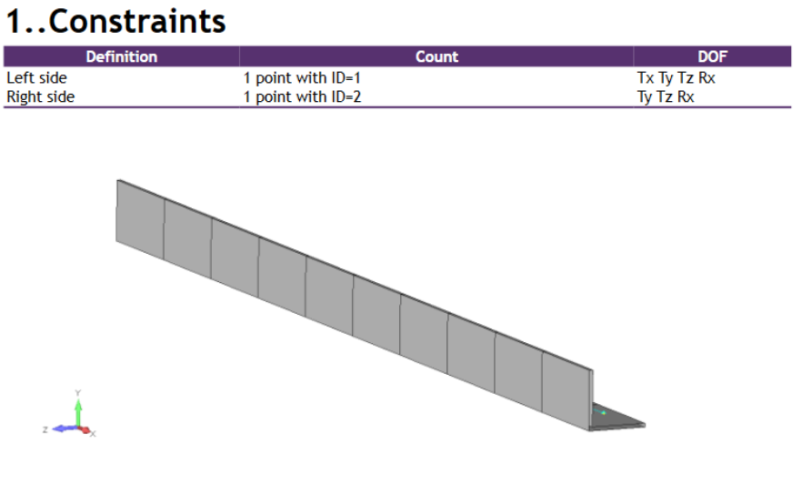
Results 

Principal Axes Moments (Figure F.11C-2)

LRFD	ASD
Muw = Mux cos α + Muy sin α = (−0.945 kip-ft)(cos 45°) + (0.540 kip-ft)(sin 45°) = −0.286 kip-ft = 3432 lbf·in	Maw = Max cos α + May sin α = (−0.734 kip-ft)(cos 45°) + (0.243 kip-ft)(sin 45°) = −0.347 kip-ft
Muz = −Mux sin α + Muy cos α = −(−0.945 kip-ft)(sin 45°) + (0.540 kip-ft)(cos 45°) = 1.05 kip-ft = 12,600 lbf·in	Maz = −Max sin α + May cos α = −(−0.734 kip-ft)(sin 45°) + (0.243 kip-ft)(cos 45°) = 0.691 kip-ft

The lateral-torsional buckling limit state controls.

M_nw = 79.4 kip-in. or 6.62 kip-ft = 79,400 lbf·in

The flexural yielding limit state controls.

M_nz = 42.0 kip-in. or 3.50 kip-ft = 42,000 lbf·in

As we can see, the principal axes moment values as well as the available flexural strengths in principal axes coincide with the results from SDC Verifier, the latter being slightly conservative due to the simplified fillet radiuses.

Any of the intermediate results can be checked as well using the calculation details functionality in SDC Verifier, so for example:

Nominal flexural strength according to the limit state of yielding:

Flexural Yielding

(from Spec. Eq. F10-1)

M_nw = 1.5 M_y

= 1.5 F_y S_wC

= 1.5 × (36 ksi) × (1.76 in.³)

= 95.0 kip-in. = 95,000 lbf·in

Nominal Flexural Strength (Leg Local Buckling, Noncompact Leg)

Nominal flexural strength according to the limit state of leg local buckling for sections with noncompact legs:

Leg Local Buckling

(from Spec. Eq. F10-6)

M_nw = F_y S_c × [2.43 − 1.72 (b/t) √(F_y / E)]

= (36 ksi) × (1.76 in.³) × [2.43 − 1.72 × 16.0 × √(36 ksi / 29,000 ksi)]

= 92.5 kip-in. = 92,500 lbf·in

For consistency with internal SDC Verifier axis naming, the major principal axis is referred to as the U-axis (represented as the W-axis in this example), and the minor principal axis is the V-axis (represented here as the Z-axis).

The intermediate results also align well, considering the simplified modeling without fillet radii.

SDC Verifier automatically identifies the governing limit states. In this case, the controlling conditions are:

• Lateral-torsional buckling for major axis flexure (U-axis)
• Flexural yielding for minor axis flexure (V-axis)

The combined effects are evaluated in the final Overall Check.

🔹 At Point B

M_w causes no stress at point B, so the stress ratio is set to zero. M_z causes tension and is taken as negative.

LRFD:

0 − (1.05 kip-ft / 3.15 kip-ft) = 0.333 ≤ 1.0 → o.k.

ASD:

0 − (0.691 kip-ft / 2.10 kip-ft) = 0.329 ≤ 1.0 → o.k.

At Point C

M_w causes tension → negative M_z causes compression → positive

LRFD:

(−0.286 kip-ft / 5.96 kip-ft) + (1.05 kip-ft / 3.15 kip-ft) = 0.285 ≤ 1.0 → o.k.

ASD:

(−0.347 kip-ft / 3.96 kip-ft) + (0.691 kip-ft / 2.10 kip-ft) = 0.241 ≤ 1.0 → o.k.

At Point A

M_w and M_z both cause compression, so both values are positive.

LRFD:

(0.286 kip-ft / 5.96 kip-ft) + (1.05 kip-ft / 3.15 kip-ft) = 0.381 ≤ 1.0 → o.k.

ASD:

(0.347 kip-ft / 3.96 kip-ft) + (0.691 kip-ft / 2.10 kip-ft) = 0.417 ≤ 1.0 → o.k.

All stress interaction ratios are below 1.0, confirming that the member is sufficient to resist the applied loads.

Point A is the critical location, as both principal axis moments contribute compressively, resulting in the highest combined effect.

SDC Verifier automatically checks the most critical stress combination.
When comparing the results from SDC Verifier with those from Example F.11C, we observe a strong agreement between the two.

The slight conservatism in SDC Verifier results is attributed to simplifications in the modeled geometry, such as the omission of fillet radii.

Conclusion

The results from SDC Verifier closely match those of AISC Example F.11C, confirming its reliability for evaluating flexural behavior in single-angle members under combined vertical and horizontal loading. Slight conservatism in the results is expected due to geometric simplifications in the FEA model, such as the omission of toe and root fillet radii.

SDC Verifier automatically identifies the governing limit states for each principal axis:

• Lateral-torsional buckling for the major axis (U-axis)

• Flexural yielding for the minor axis (V-axis)

Instead of evaluating interaction ratios across multiple locations, SDC Verifier checks the worst-case combination of internal forces. While this approach may yield slightly conservative results, it ensures a streamlined and fully automated code check.

All final interaction checks for both LRFD and ASD fall within acceptable limits, confirming that the selected L4×4×¼ angle is structurally sufficient for the applied loads.

This benchmark demonstrates SDC Verifier’s strength as a transparent, standards-based verification tool — enabling fast, accurate, and automated validation of structural designs.