
We built a minimal, realistic EC9 weld example to validate SDC Verifier: a 6061-T6 aluminium T-joint with a single fillet weld across 200 mm. Forces in all three axes generate bending about x and y. We computed throat stresses at four points and checked both weld capacity and HAZ requirements. The same setup was run in SDC Verifier 2025 R2 with identical assumptions and inputs as the hand-calc route.
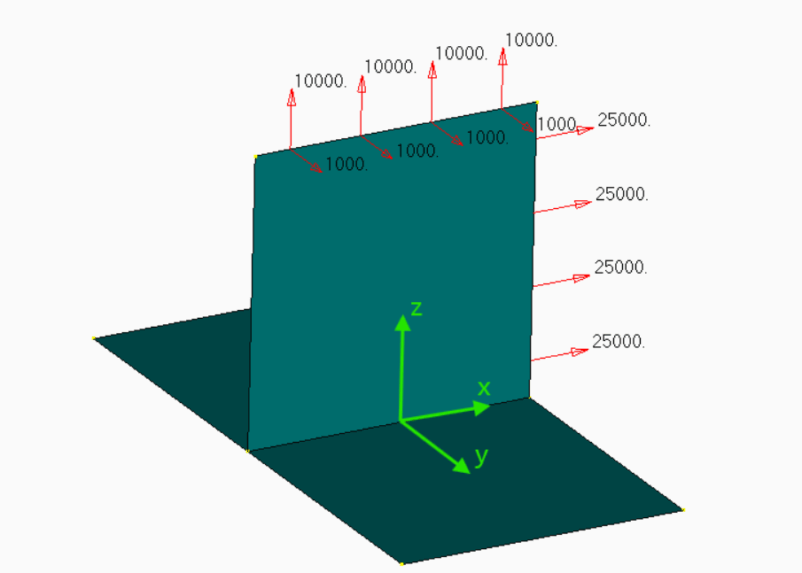
Figure 1 – Analyzed welded connection
Using the coordinate system marked on the figure above we can denote the forces acting on the weld:
Fx = 25 000 N
Fy = 1 000 N
Fz = 10 000 N
and the resultant moments:
Mx = Fy∗200 mm = 1000 N∗0.2 m = 200 Nm
My = −Fx∗100 mm = −25000 N∗0.1 m = −2500 Nm
Mz=0 Nm
The check according to Eurocode 9 consists of two design requirements that need to be verified – the design strength of the welds (as per 8.6.3.2 and 8.6.3.3) and the design strength of the Heat Affected Zone (HAZ) adjacent to a weld (as per 8.6.3.4).
To check the design of the welds one first has to calculate the stress components acting on the throat section of a fillet weld as shown on Figure 2 below.
Figure 2 – Stresses acting on the throat section of a fillet weld (Source: EN 1991-1-1:2007+A1:2009
Additionally on Figure 2 there are marked 4 points on the throat section – these are used to evaluate which combination of force and moment directions will result in a maximum stress that can later be used to evaluate the weld design resistance.
Required for further calculations are also some geometric properties of the weld throat cross-section (in relation to the coordinate system shown on Figure 1):
| Weld Angle | \( \alpha = 45^\circ \) |
|---|---|
| Weld Area | \( A = 1000\ \mathrm{mm^{2}} \) |
| Elastic Section Modulus X for points 1–2 | \( w_{x12} = 11666.7\ \mathrm{mm^{2}} \) |
| Elastic Section Modulus X for points 3–4 | \( w_{x34} = 6834.2\ \mathrm{mm^{2}} \) |
| Elastic Section Modulus Y | \( w_{y} = 33333.3\ \mathrm{mm^{2}} \) |
Note: Elastic section modulus takes a different value for points 1-2 and 3-4 due to a different distance of the extreme fiber in relation to the x-axis.
The next step is to calculate the stresses acting on the throat section in all 4 points.
In point 1:
\[ \tau_{\parallel} = \frac{F_x}{A} = 25\,\text{MPa} \]
\[ \sigma_{\perp}
= \frac{F_z}{A}\,\sin\alpha
– \frac{F_y}{A}\,\sin\alpha
– \frac{M_x}{w_{x12}}\,\sin\alpha
+ \frac{M_y}{w_y}\,\sin\alpha
= 47.28\,\text{MPa} \]
\[ \tau_{\perp}
= \frac{F_z}{A}\,\cos\alpha
+ \frac{F_y}{A}\,\cos\alpha
– \frac{M_x}{w_{x12}}\,\cos\alpha
+ \frac{M_y}{w_y}\,\cos\alpha
= 48.69\,\text{MPa} \]
\[ \sqrt{\,\sigma_{\perp}^{2}
+ 3\big(\tau_{\perp}^{2} + \tau_{\parallel}^{2}\big)}
= 105.94\,\text{MPa} \]
In point 2:
\[ \tau_{\parallel} = \frac{F_x}{A} = 25\,\text{MPa} \]
\[ \sigma_{\perp}
= \frac{F_z}{A}\,\sin\alpha
– \frac{F_y}{A}\,\sin\alpha
– \frac{M_x}{w_{x12}}\,\sin\alpha
– \frac{M_y}{w_y}\,\sin\alpha
= -58.79\,\text{MPa} \]
\[ \tau_{\perp}
= \frac{F_z}{A}\,\cos\alpha
+ \frac{F_y}{A}\,\cos\alpha
– \frac{M_x}{w_{x12}}\,\cos\alpha
– \frac{M_y}{w_y}\,\cos\alpha
= -57.38\,\text{MPa} \]
\[ \sqrt{\,\sigma_{\perp}^{2}
+ 3\big(\tau_{\perp}^{2} + \tau_{\parallel}^{2}\big)}
= 123.32\,\text{MPa} \]
In point 3:
\[ \tau_{\parallel} = \frac{F_x}{A} = 25\,\text{MPa} \]
\[ \sigma_{\perp}
= \frac{F_z}{A}\,\sin\alpha
– \frac{F_y}{A}\,\sin\alpha
– \frac{M_x}{w_{x34}}\,\sin\alpha
– \frac{M_y}{w_y}\,\sin\alpha
= -67.36\,\text{MPa} \]
\[ \tau_{\perp}
= \frac{F_z}{A}\,\cos\alpha
+ \frac{F_y}{A}\,\cos\alpha
– \frac{M_x}{w_{x34}}\,\cos\alpha
– \frac{M_y}{w_y}\,\cos\alpha
= -65.95\,\text{MPa} \]
\[ \sqrt{\,\sigma_{\perp}^{2} + 3\big(\tau_{\perp}^{2} + \tau_{\parallel}^{2}\big)}
= \color{#c1121f}{139.50\,\text{MPa}} \]
In point 4:
\[ \tau_{\parallel} = \frac{F_x}{A} = 25\,\text{MPa} \]
\[ \sigma_{\perp}
= \frac{F_z}{A}\,\sin\alpha
– \frac{F_y}{A}\,\sin\alpha
– \frac{M_x}{w_{x34}}\,\sin\alpha
+ \frac{M_y}{w_y}\,\sin\alpha
= 38.70\,\text{MPa} \]
\[ \tau_{\perp}
= \frac{F_z}{A}\,\cos\alpha
+ \frac{F_y}{A}\,\cos\alpha
– \frac{M_x}{w_{x34}}\,\cos\alpha
+ \frac{M_y}{w_y}\,\cos\alpha
= 40.12\,\text{MPa} \]
\[ \sqrt{\,\sigma_{\perp}^{2}
+ 3\big(\tau_{\perp}^{2} + \tau_{\parallel}^{2}\big)}
= 90.56\,\text{MPa} \]
As we can see the maximum equivalent stress is obtained in point 3 with a value of 139.5 MPa, which can now be used to check the design resistance of a fillet weld according to equation (8.33) from the standard:
\[ \sqrt{\,\sigma_{\perp}^{2} + 3\!\left( \tau_{\perp}^{2} + \tau_{\parallel}^{2} \right) }
\leq \frac{f_w}{\gamma_{Mw}} \]
where:
𝑓𝑤 – characteristic strength of weld metal according to Table 8.8 – in our case, with an assumption of using filler metal 5356, 𝑓𝑤=190 𝑁/𝑚𝑚2,
𝛾𝑀𝑤 – partial safety factor for welded joints according to section 8.1.1 – in our case, according to Table 8.1, 𝛾𝑀𝑤=1.25,
then:
\[ 139.5\,\text{MPa} \le \frac{190\,\text{MPa}}{1.25} = 152\,\text{MPa} \]
or using a utilization factor notation:
\[
\frac{\sqrt{\sigma_{\perp}^{2} + 3\!\left(\tau_{\perp}^{2} + \tau_{\parallel}^{2}\right)}}
{\,f_w / \gamma_{Mw}\,}
= \frac{139.5}{152}
= 0.918 \le 1
\]
Which means that the design resistance of the fillet weld fulfills the requirement from equation (8.33).
The design strength of the Heat Affected Zone (HAZ) adjacent to a weld as per section 8.6.3.4 has to be checked in two locations – in the fusion boundary (HAZ F) and in the toe of the weld (HAZ T), as shown on Figure 8.21 in the standard.
Let’s first check the HAZ F requirement. This can be done similarly as the weld strength requirement, so by checking in 4 corners of each failure plane, but to make these calculations shorter we will only show the calculations of the least favorable stress orientation combination.
Geometric properties of the failure plane in the fusion boundary at a weld angle of 0°:
| Weld Angle | α = 0° |
|---|---|
| Weld Area | A = 1414.2 mm2 |
| Elastic Section Modulus X for points 1–2 | wx12 = 21785.1 mm2 |
| Elastic Section Modulus X for points 3–4 | wx34 = 9023.7 mm2 |
| Elastic Section Modulus Y | wy = 47140.5 mm2 |
Maximum stresses in HAZ F for a weld angle of 0°:
\[ \sigma_{haz,Ed}
= \frac{F_z}{A}
- \frac{M_x}{w_{x34}}
- \frac{M_y}{w_y}
= -68.12\,\text{MPa} \]
\[ \tau_{haz,Ed}
= \frac{F_x}{A}
= 17.68\,\text{MPa} \]
\[ \sqrt{\,\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}
= 74.69\,\text{MPa} \]
where:
𝜎ℎ𝑎𝑧,𝐸𝑑 – design normal stress perpendicular to the weld axis,
𝜏ℎ𝑎𝑧,𝐸𝑑 – design shear stress parallel to the weld axis.
Using these stress values we can check the design requirements as per equations (8.39), (8.41) and (8.43), so:
\( \sigma_{haz,Ed} \le \frac{f_{u,haz}}{\gamma_{Mw}} \),
\( \tau_{haz,Ed} \le \frac{f_{v,haz}}{\gamma_{Mw}} \),
\( \sqrt{\sigma_{haz,Ed}^{2}+3\,\tau_{haz,Ed}^{2}} \le \frac{f_{u,haz}}{\gamma_{Mw}} \)
where:
𝑓𝑢,ℎ𝑎𝑧 – characteristic strength HAZ as per 8.6.2 – in our case according to Table 3.2a for alloy 6061 with temper T6 and plate thickness ≤ 12.5 mm, 𝑓𝑢,ℎ𝑎𝑧=175 𝑁/𝑚𝑚2,
and, as per 8.6.2:
\[ f_{v,haz} = \frac{f_{u,haz}}{\sqrt{3}} = 101.04\ \mathrm{N/mm^{2}} \]
so, using a utilization factor notation:
\[
\frac{\sigma_{haz,Ed}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{68.12\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.486 \le 1
\]
\[
\frac{\tau_{haz,Ed}}{\,f_{v,haz}/\gamma_{Mw}\,}
= \frac{17.68\,\text{MPa}}{101.04\,\text{MPa}/1.25}
= 0.219 \le 1
\]
\[
\frac{\sqrt{\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{74.69\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.534 \le 1
\]
Geometric properties of the failure plane in the fusion boundary at a weld angle of 90°:
| Weld Angle | α = 90° |
|---|---|
| Weld Area | A = 1414.2 mm2 |
| Elastic Section Modulus X* | wx = 1666.7 mm2 |
| Elastic Section Modulus Z | wy = 47140.5 mm2 |
| Polar Moment of Inertia | Ip = 4 719 937.8 mm4 |
| Maximum Radius | rmax = 100.1 mm |
| Gamma Angle | γ = 2.02° |
| * X modulus taken with the X-axis through the mid-plane of the failure surface (conservative simplification). | |
*Note: Assumed conservative simplification where the X axis (parallel to the weld axis) goes through the middle of the analyzed failure plane.
Maximum stresses in HAZ F for a weld angle of 90°:
\[ \sigma_{haz,Ed}
= \frac{F_y}{A} + \frac{M_x}{w_{x}}
= 120.70\,\text{MPa} \]
\[ \tau_{haz,Ed}
= \frac{F_x}{A} + \frac{M_y\, r_{\max}}{I_p}\,\sin\gamma
= 19.54\,\text{MPa} \]
\[ \sqrt{\,\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}
= 125.36\,\text{MPa} \]
so, checking the design requirements as per equations (8.39), (8.41) and (8.43), using a utilization factor notation:
\[
\frac{\sigma_{haz,Ed}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{120.70\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.862 \le 1
\]
\[
\frac{\tau_{haz,Ed}}{\,f_{v,haz}/\gamma_{Mw}\,}
= \frac{19.54\,\text{MPa}}{101.04\,\text{MPa}/1.25}
= 0.242 \le 1
\]
\[
\frac{\sqrt{\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{125.36\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.895 \le 1
\]
Now let’s move on to the HAZ T requirement. As mentioned in the standard in 8.6.3.4 this requirement has to be checked at the toe of the weld (full cross section), so in our case both in the bottom plate and in the top plate.
Starting with the top plate, the geometric properties of the cross-section (the base material cross-section with the coordinate system in the middle of it):
| Weld Part Area | A = 2 000 mm2 |
|---|---|
| Elastic Section Modulus X | wx = 3 333.3 mm2 |
| Elastic Section Modulus Y | wy = 66 666.7 mm2 |
| Polar Moment of Inertia | Ip = 6 683 333.1 mm4 |
| Maximum Radius | rmax = 100.1 mm |
| Gamma Angle | γ = 2.86° |
Maximum stresses in HAZ T in the top plate:
\[ \sigma_{haz,Ed}
= \frac{F_z}{A} + \frac{M_x}{w_{x}} + \frac{M_y}{w_{y}}
= 102.50\,\text{MPa} \]
\[ \tau_{haz,Ed}
= \frac{F_x}{A}
= 12.50\,\text{MPa} \]
\[ \sqrt{\,\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}
= 104.78\,\text{MPa} \]
design requirements as per equations (8.39), (8.41) and (8.43), using a utilization factor notation:
\[
\frac{\sigma_{haz,Ed}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{102.50\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.732 \le 1
\]
\[
\frac{\tau_{haz,Ed}}{\,f_{v,haz}/\gamma_{Mw}\,}
= \frac{12.50\,\text{MPa}}{101.04\,\text{MPa}/1.25}
= 0.155 \le 1
\]
\[
\frac{\sqrt{\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{104.78\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.748 \le 1
\]
Geometric properties of the bottom plate cross-section:
| Weld Part Area | A = 2 000 mm2 |
|---|---|
| Elastic Section Modulus X | wx = 3 333.3 mm2 |
| Elastic Section Modulus Z | wz = 66 666.7 mm2 |
| Polar Moment of Inertia | Ip = 6 683 333.1 mm4 |
| Maximum Radius | rmax = 100.1 mm |
| Gamma Angle | γ = 2.86° |
Maximum stresses in HAZ T in the bottom plate:
\[ \sigma_{haz,Ed}
= \frac{F_y}{A} + \frac{M_x}{w_x}
= 60.50\,\text{MPa} \]
\[ \tau_{haz,Ed}
= \frac{F_x}{A} + \frac{M_y\, r_{\max}}{I_p}\,\sin\gamma
= 14.37\,\text{MPa} \]
\[ \sqrt{\,\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}
= 65.42\,\text{MPa} \]
design requirements as per equations (8.39), (8.41) and (8.43), using a utilization factor notation:
\[
\frac{\sigma_{haz,Ed}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{60.50\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.432 \le 1
\]
\[
\frac{\tau_{haz,Ed}}{\,f_{v,haz}/\gamma_{Mw}\,}
= \frac{14.37\,\text{MPa}}{101.04\,\text{MPa}/1.25}
= 0.178 \le 1
\]
\[
\frac{\sqrt{\sigma_{haz,Ed}^{2} + 3\,\tau_{haz,Ed}^{2}}}{\,f_{u,haz}/\gamma_{Mw}\,}
= \frac{65.42\,\text{MPa}}{175\,\text{MPa}/1.25}
= 0.467 \le 1
\]
As we can see the design strength of the HAZ adjacent to the weld (both HAZ F and HAZ T) fulfills the requirements from equations (8.39), (8.41) and (8.43).
This means that all design requirements have been fulfilled and the design of the weld according to Eurocode 9 is correct.
Collecting all the maximum results for each design requirement we get the following:
| Design Requirement | Maximum Utilization Factor |
|---|---|
| Design strength of the weld | 0.918 |
| Design strength of HAZ F | 0.895 |
| Design strength of HAZ T | 0.748 |
All results are calculated using SDC Verifier 2025 R2.
The model was created in SDC Verifier using the same geometry, material and other standard related inputs as for the hand calculations.
Materials
Properties
Loads
Constraints
Standard related inputs
Final results
As we can see using SDC Verifier we arrive at the same conclusion, which is that the designed weld passes all the requirements according to Eurocode 9.
All the intermediate results can be checked as well using SDC Verifier, so for example:
– Equivalent stresses in the weld (all 4 points):
– Equivalent stresses in HAZ F (all 4 points for weld angle 0°, maximum result for 90°):
– Stresses in HAZ T in the top plate (where 𝑋=𝜏ℎ𝑎𝑧,𝐸𝑑, 𝑌=𝜎ℎ𝑎𝑧,𝐸𝑑):
– Stresses in HAZ T in the bottom plate:
As we can see from the table below the results from hand calculations and from SDC Verifier align perfectly, which proves a high accuracy of the SDC Verifier implementation of the weld check according to EN 1991-1-1:2007+A1:2009
| Design Requirement | Maximum Utilization Factor | |
|---|---|---|
| Hand Calculations | SDC Verifier | |
| Design strength of the weld | 0.918 | 0.918 |
| Design strength of HAZ F | 0.895 | 0.895 |
| Design strength of HAZ T | 0.748 | 0.748 |
Additionally, the intermediate results shown in the previous chapter can be compared, which show only minor discrepancies due to rounding and numerical errors.
The great benefit of using SDC Verifier for this check is that obtaining the results took only a fraction of the time required for performing it with hand calculations.
The benchmark confirms SDC Verifier’s Eurocode 9 §8.6 implementation is numerically consistent with the code. For the given load case, the design meets weld and HAZ criteria with the governing utilization ≤ 0.918. Engineers get clause-mapped details for audit; non-engineers get a clear pass/fail answer—without spreadsheets.
Stay updated with the latest in structural verification, engineering insights, and SDC Verifier updates.