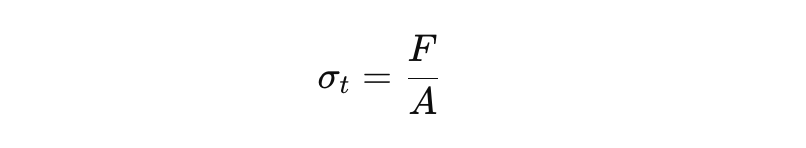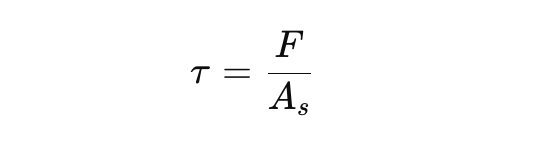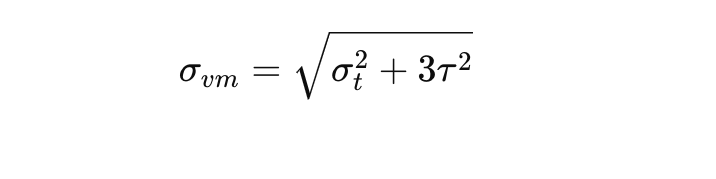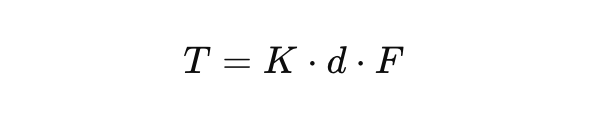Bolt Loading Calculations: Factors to Consider

Every structure, machine, or piece of equipment relies on bolts to hold critical connections together, often under immense forces. Accurate bolt loading calculations are key to ensuring the safety and durability of bolted joints, especially under extreme conditions. From accommodating tensile forces to countering shear stresses, calculating these loads is essential for the safety and durability of any design.
In this article, we’ll explore the key factors engineers need to consider when assessing bolt loads, providing a detailed guide to understanding the forces that impact bolt performance.
Read previous articles about bolts:
- Standards for Bolts: A Comprehensive Guide
- Understanding Bolt Specifications: A Beginner’s Guide
- Bolt Strength Calculations: Understanding the Fundamentals
- Bolt Stress Calculations: A Step-by-Step Guide
What is Bolt Loading?
Bolt loading is the combined force acting on the bolts in a joint, influenced by external loads and the application geometry. The loading forces result from external loads applied to the connected components.
Calculating bolt loads ensures that the bolts can withstand the applied stresses without failing, loosening, or over-stretching. The three most common types of bolt loads are tension, shear, and combined loading. When external loads are applied to a joint, they are transferred through the connected parts to the bolts, which then bear the stresses based on the load path. This path determines how the forces are distributed among the bolts, affecting their performance. Each type of load has a distinct effect on the bolt’s integrity, making it vital to consider these factors during design and analysis.
Types of Loads in Bolt Loading Calculations
1. Tensile Load
A tensile load occurs when forces pull the connected components away from each other, causing the bolt to elongate. This load is common in applications where the bolt resists forces along its axis, such as in tension joints.
- Effect on Bolts: When a bolt experiences tensile loading, the stress on the bolt is highest at the root of the thread. Overloading in tension can cause bolt failure due to material deformation or fracture.
- Calculating Tensile Load: Tensile stress (σt) can be calculated using the formula:
Where:
-
- F is the applied force in Newtons (N).
- A is the tensile stress area of the bolt, typically the minimum cross-sectional area of the bolt’s threaded portion.
2. Shear Load
Shear load acts perpendicular to the axis of the bolt and tends to cut the bolt in two. Shear loads occur in joints where forces act parallel to the surfaces being fastened, such as in lap joints.
- Effect on Bolts: Bolts can experience shear failure if the load exceeds the material’s shear strength. In this case, the bolt may experience slippage or be physically sheared off between connected plates.
- Calculating Shear Load: Shear stress (τ) is calculated as:
Where:
-
- F is the applied force in Newtons (N).
- As is the shear area, which is typically the cross-sectional area of the bolt’s unthreaded portion for single shear planes.
Single vs. Double Shear: In a single shear joint, the bolt only experiences a shear force along one plane. In a double shear joint, the bolt is loaded in two planes, which distributes the load across two areas, increasing the bolt’s capacity to resist shear.
3. Combined Loading (Tension and Shear)
In many real-world applications, bolts are subject to both tensile and shear loads simultaneously. Combined loading complicates the analysis because the bolt must resist both axial and lateral forces. This scenario often arises in complex joints such as flange connections or bolted structures subject to both tensile forces
and lateral forces.
- Effect on Bolts: Under combined loading, the bolt is more susceptible to failure since it must handle multiple stress components. The interaction between tensile and shear stresses reduces the bolt’s capacity to withstand either load type independently.
- Calculating Combined Stress: Combined loading is evaluated using the von Mises stress or a similar interaction equation. This method combines stresses from different directions, along with the tensile stress introduced by the bolt preload, into a single equivalent stress value. By accounting for all these factors, this approach helps ensure that the bolt can handle the complex load conditions without failing:
Where:
- σvm is the von Mises equivalent stress.
- σt is the tensile stress.
- τ is the shear stress.
Factors influencing Bolt Strength to Consider in Bolt Loading Calculations
1. Material Properties
The material of the bolt plays a significant role in determining its strength which as a result shows how much load it can handle. Common bolt materials include carbon steel, stainless steel, and alloy steel, each with different tensile strengths, shear strengths, and fatigue limits. Understanding the mechanical properties of the material is crucial in ensuring that the bolt can withstand the applied loads without failure.
- Tensile Strength: It is the maximum amount of tensile stress that a bolt can endure before failing.
- Shear Strength: It is the bolt’s resistance to shearing forces.
- Fatigue Strength: It refers to the bolt’s ability to withstand cyclic loading over time, which is critical for dynamic applications. Also, SDC Verifier’s Fatigue App can simplify the checks regarding fatigue issues.
2. Thread Engagement
The amount of thread engagement between the bolt and the nut or tapped hole significantly impacts the bolt’s strength resulting in its load-bearing capacity. Insufficient thread engagement can lead to thread stripping, especially in high-tensile bolts, where the loads are more severe. A higher percentage of thread engagement allows for better load distribution and reduces this risk.
- Ideal Engagement: Typically, a bolt should engage with at least 6-7 threads to maximize tensile strength.
- Threaded vs. Unthreaded Portion: Bolts are stronger in the unthreaded shank section, which resists shear more effectively than the threaded portion. In high-shear applications, it is crucial to position the unthreaded portion (shank) in the shear plane to prevent premature failure.
3. Preload and Tightening Torque
Preload is the tension introduced in a bolt when it is tightened. Applying the correct tightening torque ensures the bolt is preloaded sufficiently to resist external forces without becoming loose. A bolt’s preload is influenced by the tightening method (e.g., torque wrench, stretch measurement) and friction between the bolt’s threads and mating surface.
- Torque-Tension Relationship: Preload is calculated using the torque applied to the bolt, often using empirical formulas such as:
Where:
- is the applied torque in Newton-meters (N).
Kis the friction factor (depending on surface condition and lubrication).
d is the bolt diameter in meters (m).
Fis the preload force in Newtons (N).
Preload Importance: A well-preloaded bolt not only resists external tensile forces better, preventing joint separation, but also helps to transfer shear forces through friction between the plates, reducing the reliance on the bolt’s shear resistance and lowering the likelihood of fatigue failure.
4. Environmental Conditions
Environmental factors such as temperature, corrosion, and vibration affect bolt strength and its ability to handle certain loads. High temperatures can reduce the material strength of the bolt, while corrosion weakens the bolt over time, particularly in outdoor or marine environments. Vibration can cause bolt loosening, which is a common issue in dynamic applications.
To mitigate this, techniques such as using thread-locking compounds or locking washers are often employed. These solutions help maintain bolt tension and prevent loosening, ensuring the joint remains secure under vibratory conditions.
- Thermal Expansion: Temperature fluctuations can cause bolts to expand or contract, leading to additional stresses or loosening. If the bolt and the material it joins have different coefficients of thermal expansion, this mismatch can lead to significant joint issues, especially under high-temperature variations.
- Corrosion Protection: Using corrosion-resistant materials (e.g., stainless steel or coatings) helps maintain bolt strength in harsh conditions.
5. Bolt Size and Geometry
The diameter, length, and thread pitch of a bolt affect its capacity to handle loads. Larger diameter bolts can handle more loads due to a greater cross-sectional area, while longer bolts may experience bending or buckling under certain loads.
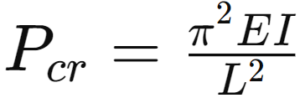
Euler’s buckling formula
A general guideline is to perform buckling analysis when the slenderness ratio (the length of the bolt divided by its radius of gyration) exceeds a critical value. Euler’s buckling formula, can be used to determine the critical load at which buckling may occur.
- Bolt Grade: Higher-grade bolts (e.g., Grade 8) have higher tensile and shear strength compared to lower-grade bolts (e.g., Grade 2).
- Thread Pitch: Fine-thread bolts have higher tensile strength but lower shear strength compared to coarse-thread bolts. Additionally, thread pitch affects how preload is applied and how load is distributed across the threads. Fine-thread bolts allow for more precise control of preload, which is important in high-strength applications, as it helps ensure even load distribution and reduces the risk of loosening.
The global geometry of the structure and local geometry/shape of the connection will affect how much load will be transferred through a certain bolt. Additionally, the more bolts you have, the less load will act on each of them, assuming an even load distribution.
Conclusion
Accurate bolt loading calculations are essential for structural engineers to ensure the integrity of bolted joints under various types of loads. Understanding how tensile, shear, and combined loads affect bolts, as well as considering factors like material properties, thread engagement, and environmental conditions, enables engineers to design safer, more reliable connections. By factoring in these variables, you can ensure that your bolted joints perform optimally under the conditions they will face.