What Are Element and Node Sets in FEA?

Finite Element Analysis (FEA) is a powerful computational tool used by engineers to simulate and analyze the behavior of structures under various conditions. From the simplest beam to the most complex system, FEA allows engineers to evaluate the performance of designs before physical testing.

Element and node sets in FEA are fundamental components that define the discretized model of a structure. Nodes and elements are essential to the analysis, as they form the basis of the entire model, determining how the structure is represented and how various properties, loads, and constraints are applied to it. In this article, we’ll explore the key components of FEA such as elements and nodes, their purpose, and how they work together in the analysis process.

(source)

Understanding Element and Node Sets?

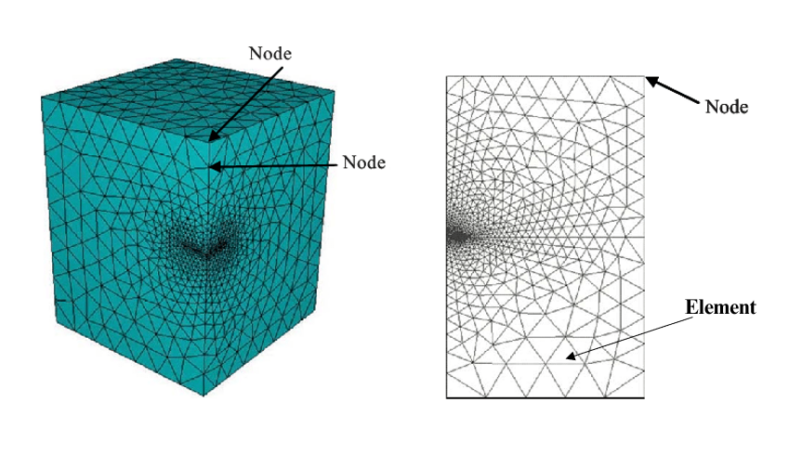
In FEA, the physical model of a structure is transformed into a set of mathematical equations that can be solved numerically. This process involves discretization, where the continuous structure is broken down into smaller, manageable elements. Each element is connected to others at specific points known as nodes.

The solver then constructs the stiffness matrix, which represents the relationship between forces and displacements within the system. This matrix, along with other components like the global matrix, forms the foundation of the numerical solution. Element and node sets define how the structure is discretized, allowing for the assignment of specific properties, loads, and constraints to different regions of the model.

• Elements are small building blocks of the model, connecting nodes to form shapes like beams, shells, or solids (is a small subdivision of the overall structure that connects nodes)
• Nodes are specific points in space that define the geometry of the model and serve as the connection points between elements. They are where calculations are performed in FEA, and results are computed. Nodes also play a crucial role in setting boundary conditions, such as defining the degrees of freedom for displacements and rotations, or applying loads.

Crucial about Element and Node Sets to Remember

• Elements interact with each other through nodes – Nodes serve as the connection points between elements, defining how they interact within the model.
• Loads and constraints are applied only to nodes – From the solver’s perspective, boundary conditions (such as displacements, rotations, and loads) are applied to nodes, not the elements themselves.
• Element deformation is defined solely by the translation of its nodes – The deformation of an element is determined by the movement of its nodes in response to applied loads and boundary conditions.
• Deformation is determined by solving a system of algebraic equations – The number of equations in this system depends on the total number of nodes and their degrees of freedom (DOF). The solver solves these equations to determine the behavior of the structure.
• The purpose of the element – An element represents a specific part of the structure and defines its material properties, stress distribution, and other physical characteristics. Elements are used to model the behavior of the structure under different conditions.

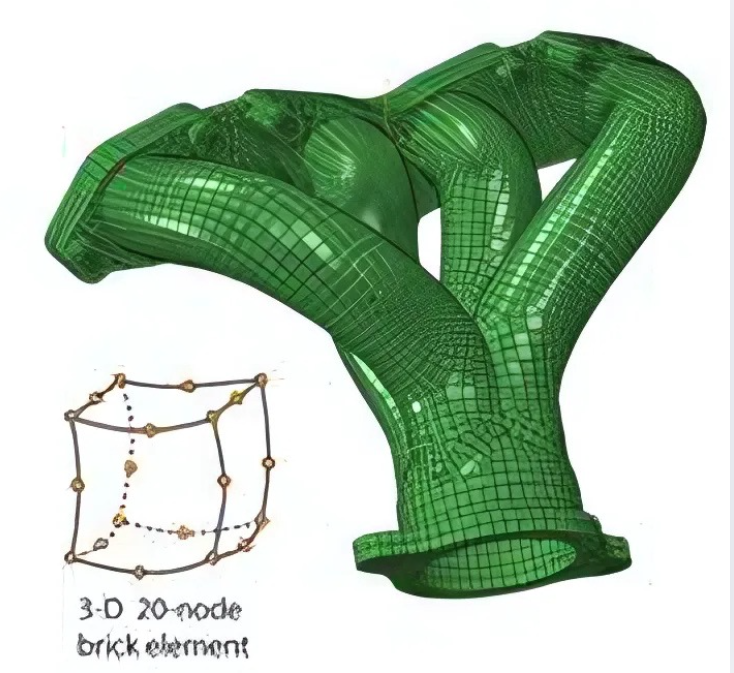
Example: 3-dimensional brick element which contains 20 nodes

(source)

Elements and Node Sets in FEA Software

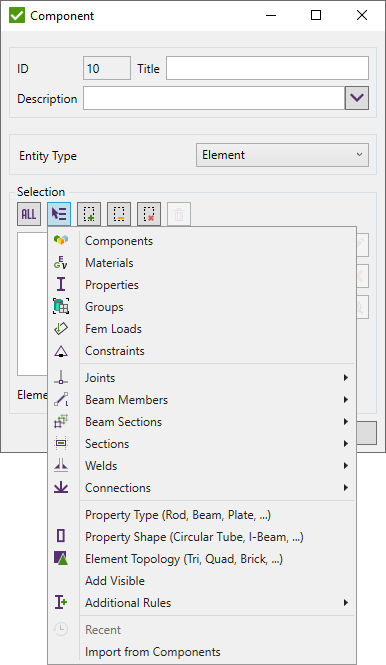
In structural design and analysis software SDC Verifier, elements and nodes can be added directly through the model tree by selecting Model – Components – Add. Users can assign a title to the component and choose whether the component will consist of nodes or elements. This functionality enhances model organization, making it easier to manage complex geometries and load cases.

Types of Elements

Finite elements in FEA can be categorized into three main types:

1. 1D Elements (Beams)

These are simple line elements that connect two nodes. They are typically used for structures like beams and trusses, where the element’s cross-section is small compared to its length. These elements have only one direction of deformation, along the length of the element.

(source)

1. 2D Elements (Shells)

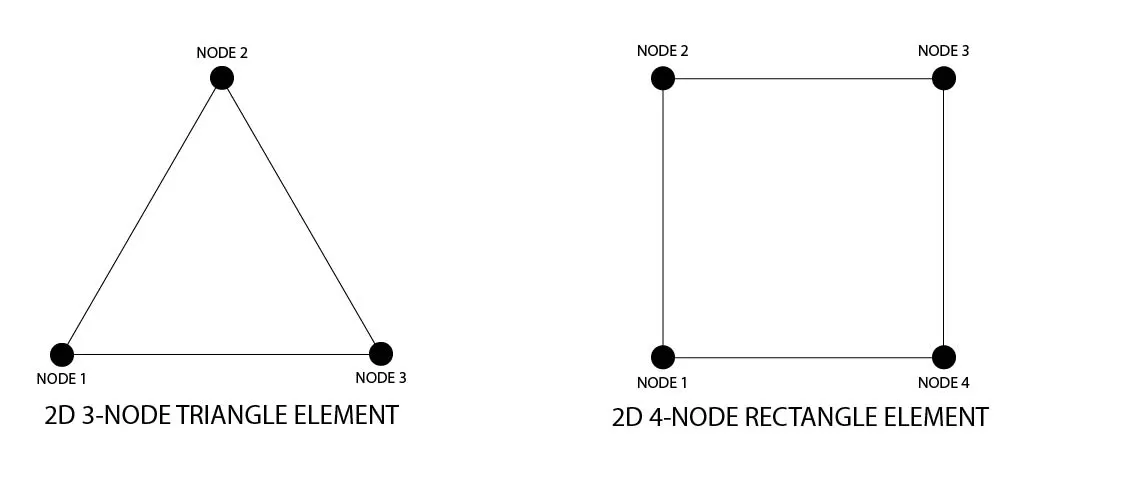
These 2D elements come in shapes like triangles (TRI) or quadrilaterals (QUAD). They are useful for modeling surfaces such as plates or shells, where the thickness is small compared to the other dimensions. However, their application is governed by assumptions like plane stress, plane strain, or shell theory, which determine how these elements behave under different conditions.

Additionally, there are membrane elements, which are a type of 2D element, used to model structures that resist in-plane forces but not out-of-plane bending.

(source)

1. 3D Elements (Solids)

These elements represent volumes and can be based on tetrahedrons (TET) or hexahedrons (HEX) shapes. They’re essential for modeling solid objects in three dimensions.

Each element type connects at points called nodes, which define the element’s geometry and connectivity. Higher-order elements have additional nodes, which allow for a more accurate representation of curved geometries and provide improved stress gradients. These elements are particularly advantageous for modeling complex shapes, as they enable better approximation of non-linear behaviors and more precise results in areas of high stress variation.

However, elements themselves are a mathematical abstraction; the real calculations revolve around the nodes and their interactions. This helps represent and solve complex structural behavior effectively.

The Importance of Choosing the Right Element Type

Selecting the appropriate element type is crucial to balancing accuracy and computational efficiency in FEA. The solver solves a system of equations that is determined by the number of nodes and their degrees of freedom (DOF). Therefore, the more nodes you have, the more time it takes to solve the model. Here’s how different element types impact this balance:

• 1D Beam Elements: These elements are ideal for simple structures primarily experiencing bending, tension, or compression. They have fewer nodes compared to 2D or 3D elements, making them computationally efficient. However, they fail to capture local effects like stress concentrations or torsion, making them unsuitable for more complex geometries.
• 2D Planar Elements: Commonly used for thin structures, such as sheet metal, these elements provide a good balance between accuracy and computational speed. They are still more computationally efficient than 3D solid elements but cannot account for out-of-plane stresses or complex three-dimensional effects.
• 3D Solid Elements: Best suited for analyzing complex geometries and load cases involving out-of-plane stresses, these elements are computationally demanding. They have many more nodes and degrees of freedom, resulting in a higher number of equations for the solver to solve. This requires significantly more computational resources and time, so 3D solid elements should be reserved for cases where simpler element types are inadequate.

Conclusion

Element and node sets are fundamental components that define the discretized model of a structure in FEA. Choosing the right element type further ensures a balance between computational efficiency and accuracy, catering to the unique demands of each project.

Whether you’re working with 1D beams, 2D shells, or 3D solids, understanding and leveraging element and node sets will empower you to create more efficient, accurate, and manageable FEA models. With software like SDC Verifier offering intuitive tools for managing components, the process becomes even faster, saving valuable time and resources in engineering analysis.