What is FEM in Structural Analysis?

Finite Element Method (FEM) is a computational technique widely used in structural analysis to model and evaluate complex structures. FEM allows engineers to simulate how structures will respond to different loading conditions, including stress, strain, and displacement.

In this article, we will explore the basics of FEM in structural analysis, its mathematical foundation, its types, and the process of applying it. Additionally, we will touch on the benefits and limitations of FEM in structural evaluation.

Understanding the Basics of FEM

Finite Element Method (FEM) is a numerical approach that divides a complex structure into smaller, simpler parts called finite elements. A set of equations governs these elements based on physical laws. By solving these equations, FEM helps engineers approximate the behavior of the entire structure. The goal is to predict how forces, pressures, and displacements affect it.

One of FEM’s primary strengths is its ability to handle complex geometries, materials, and boundary conditions, making it a versatile tool for a wide range of engineering applications. FEM works by creating a finite element mesh, a network of smaller parts that helps simulate and analyze local effects and their impact on the overall structure.

Software like SDC Verifier further simplify this process by integrating automatic compliance checks with industry standards, reducing the risk of manual errors in structural verification.

For further insight, watch this discussion by mathematician Gilbert Strang from MIT, as he delves into the origins of FEM and its evolution, as well as the challenges in applying it to fluid and gas problems.

The Role of FEM in Structural Analysis

FEM plays a vital role in structural analysis by transforming a continuous structure into a set of discrete elements, allowing for the detailed study of each part. Engineers use FEM to predict how a structure will respond to various load conditions, whether static or dynamic forces.

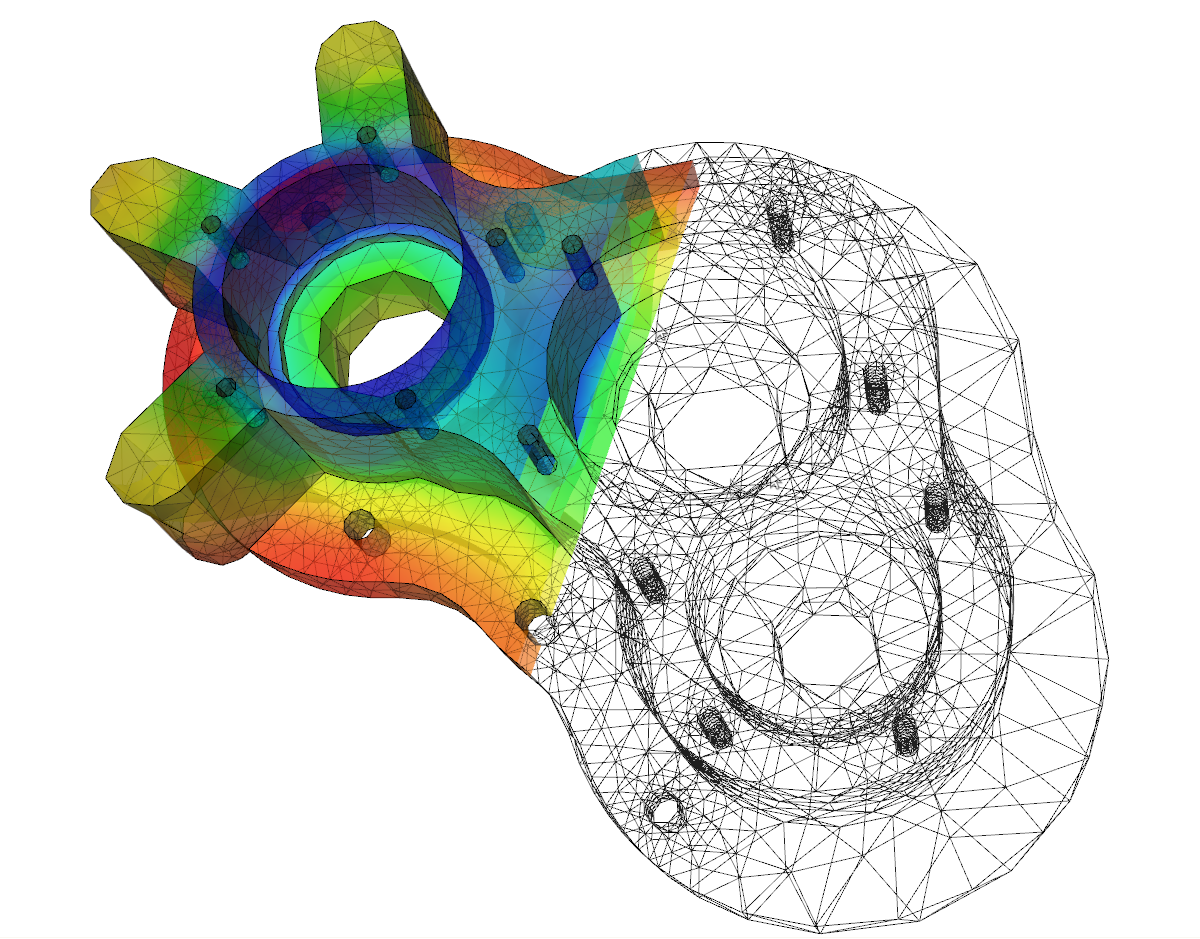
The image below showcases the practical application of FEM, with a meshed component analyzed for stress distribution, visualized through color-coded stress gradients.

Image: jousefmurad.com

By simplifying complex structures into manageable elements, engineers can make precise predictions about how loads will affect the structure, ensuring stability and safety.

FEM is particularly effective in handling real-world scenarios that involve curved material behavior or complex boundary conditions, such as bridges, high-rise buildings, or automotive crash simulations. Mesh generation within FEM enables engineers to evaluate stress, strain, and failure points within a structure, optimizing designs for safety and efficiency.

Software solutions like SDC Verifier enhance this process by providing engineers with comprehensive reporting tools that align with industry standards, streamlining the analysis workflow.

The Mathematical Foundation of FEM

Principle of Minimum Potential Energy

At the core of FEM is the Principle of Minimum Potential Energy. This principle states that a structure is in equilibrium when its total potential energy is minimized. When a structure deforms due to applied loads, it stores potential energy.

FEM applies this principle by minimizing the stored energy in each finite element, which allows engineers to predict how the structure will behave under various loading conditions.

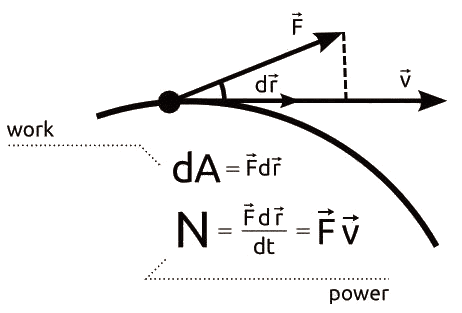
The diagram below illustrates the relationship between work, force, and displacement in mechanical systems, which is fundamental to understanding energy principles in FEM.

Image: researchgate.net

Discretization in FEM

Discretization is a fundamental step in FEM, where the continuous system (structure) is divided into finite elements. Each element has its own geometry, material properties, and relationships with neighboring elements. By discretizing the structure, engineers transform the problem of analyzing the entire system into solving a set of smaller, interconnected problems.

The accuracy of FEM depends heavily on the type and size of the finite elements used. Engineers must carefully select element shapes (e.g., triangles, tetrahedrons) and sizes to balance computational efficiency with the precision of results. Proper meshing is crucial for capturing the correct behavior of the structure and minimizing errors in simulation.

Different Types of FEM

Linear FEM

Linear FEM assumes that the relationship between applied loads and resulting displacements is proportional, meaning the structure’s response is elastic and follows Hooke’s Law. This method is commonly used when the structure’s behavior remains within the elastic range, where stress and strain are directly proportional.

Engineers often apply linear FEM to simpler problems, such as beams, trusses, and frames, in fields like civil, mechanical, and aerospace engineering. Its advantage lies in the simplicity and speed of computation, making it efficient for many practical applications. However, linear FEM is limited when dealing with complex phenomena such as plasticity, large deformations, or material failure.

Non-linear FEM

When structures undergo large deformations, or when materials exhibit non-linear stress-strain behavior, non-linear FEM is required. This method is essential for accurately modeling real-world situations where the assumptions of linear FEM no longer apply, such as in crash simulations, buckling analysis, or the study of plastic deformation.

Non-linear FEM, though more computationally intensive, provides a more realistic assessment of structural behavior under extreme conditions. Engineers must account for factors like material plasticity, creep, and contact between parts to ensure accurate results.

Despite the increased complexity, non-linear FEM is critical for designing safer and more reliable structures in fields such as automotive safety and high-performance engineering.

The Process of FEM in Structural Analysis

Pre-processing Stage

During the pre-processing stage, engineers define the structure’s geometry, assign material properties, and generate the finite element mesh. This involves converting the physical model of the structure into a mathematical one that can be solved using FEM. Engineers also apply boundary conditions and loads to simulate real-world operating conditions.

At this stage, engineers may refine the mesh to improve the accuracy of the analysis, especially in areas where stress concentrations are expected. This step helps ensure that the FEM results are reliable and converge to an accurate solution.

Solution Stage

In the solution stage, the system of equations governing the behavior of each element is solved iteratively using numerical methods. This step calculates displacements, stresses, and strains across the structure. The results offer a detailed understanding of how the structure responds to applied loads, providing crucial information for design and verification.

Engineers may also conduct sensitivity analysis during this phase, assessing how changes in material properties, geometry, or boundary conditions affect the structural response. This allows them to fine-tune the design for improved performance.

Post-processing Stage

In the post-processing stage, the results of the FEM analysis are visualized and interpreted. Engineers use software to create visual representations of the structure’s deformation, stress distribution, and critical areas. These visualizations help engineers assess whether the design meets safety standards and performance criteria.

Post-processing also includes fatigue analysis, which evaluates the structure’s durability under repeated loading conditions. By predicting potential failure points due to fatigue, engineers can make necessary design modifications to enhance the structure’s longevity and reliability.

Benefits and Limitations of FEM in Structural Analysis

Advantages of Using FEM

• Accurate Predictions: FEM enables engineers to make highly accurate predictions about how structures will respond to different loads, ensuring safety and performance, especially in critical applications like aerospace and civil engineering.

• Design Optimization: The detailed insight into stress, strain, and failure modes allows engineers to optimize designs, improving safety while reducing overdesign and material costs.

• Virtual Prototyping: FEM reduces the need for costly physical prototypes by allowing engineers to test designs virtually under various load conditions, speeding up the design process and facilitating multiple iterations.

Potential Drawbacks of FEM

• Cost and Complexity: FEM requires specialized software and hardware, which can be costly for smaller firms. Additionally, the complexity of the software may present a steep learning curve for engineers unfamiliar with the method.

• Accuracy Dependence: The accuracy of FEM results relies heavily on correct assumptions, material properties, and mesh quality. Poor meshing or incorrect material modeling can lead to errors in analysis, compromising the safety and integrity of the structure.

Conclusion

FEM is a powerful and versatile method for structural analysis, allowing engineers to simulate and evaluate complex systems with great precision. A strong understanding of FEM principles, from mesh generation to post-processing, is essential for optimizing designs and ensuring structural integrity.

While FEM offers many advantages, its limitations, such as cost and complexity, must be carefully managed. By using advanced tools like SDC Verifier, which integrate FEM with automated code-checking and reporting, engineers can streamline their workflows and ensure compliance with industry standards.