Parametric Geometry in Structural Design: Efficiency, Precision, and Optimization

Parametric geometry is revolutionizing structural design and optimization, offering engineers a cutting-edge approach to modeling and problem-solving. By embedding design logic and constraints directly into the geometry, parametric tools enable efficient iteration, precision, and innovative solutions.
This article explores the significance of parametric geometry, its role in structural optimization, and how it enhances the design process.
What is Parametric Geometry?
Parametric geometry uses parametric equations to describe geometric shapes and forms, extending beyond curves and 2D representations to include 3D shapes and solids. Namely, parametric modeling is a modeling process that can change the shape of model geometry as soon as the dimension value is modified.
In structural engineering, parametric geometry uses parametric design principles to create and optimize structures. This approach uses algorithms and computational tools to define and manipulate geometric parameters, allowing engineers to explore multiple design possibilities and optimize structural performance.
Moreover, parametric modeling incorporates dimension-driven constraints and relationships between geometric entities. These constraints and relationships define how different parts of the model interact with each other. For example:
- Constraints: These are rules that govern the relationships between different geometric entities. They can be dimensional (e.g., length, angle) or geometric (e.g., parallelism, perpendicularity).
- Dependencies: These define how changes in one parameter affect other parameters. For instance, changing the length of one side of a rectangle might automatically adjust the length of the opposite side to maintain symmetry.
- Relationships: These are connections between different parts of the model that ensure consistency. For example, if two lines are constrained to be parallel, changing the angle of one line will automatically adjust the other to maintain parallelism.
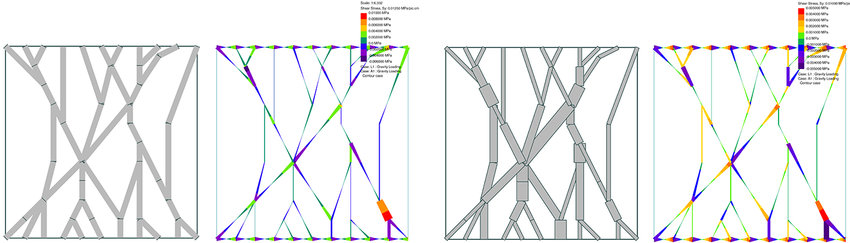
Image: Structural analysis of parametric geometry with material properties, source
Applications of Parametric Geometry in Structural Optimization
Parametric geometry offers a versatile approach to addressing challenges in structural design, enabling engineers to achieve optimized solutions with greater efficiency. Below are key applications where parametric geometry has proven invaluable in structural optimization:
1. Topology Optimization for Material Efficiency
Parametric tools enable engineers to define geometry based on specific performance metrics, such as stress distribution, load paths, and weight-to-strength ratios.
For example, engineers can use parametric modeling combined with topology optimization to reduce weight, cost, and manufacturing time by iteratively adjusting the geometry to ensure stresses, stability, and serviceability remain within allowable limits.
2. Adaptive Load Path Analysis
Structural systems often need to respond to varying load conditions. Parametric geometry allows fine-tuning elements like beams, columns, or panels; namely, parametric modeling focuses on geometric modifications, such as cross-sections or plate shapes, and does not directly change material properties.
This ensures that the load is distributed efficiently, reducing stress concentrations and improving overall performance.
3. Dynamic Design Iteration
In traditional workflows, modifying a design to meet new criteria can be time-consuming and error prone. With parametric geometry, engineers can quickly explore multiple configurations by changing input variables such as dimensions and angles.
Each iteration adapts automatically while adhering to predefined constraints, allowing for rapid prototyping and evaluation of design alternatives.
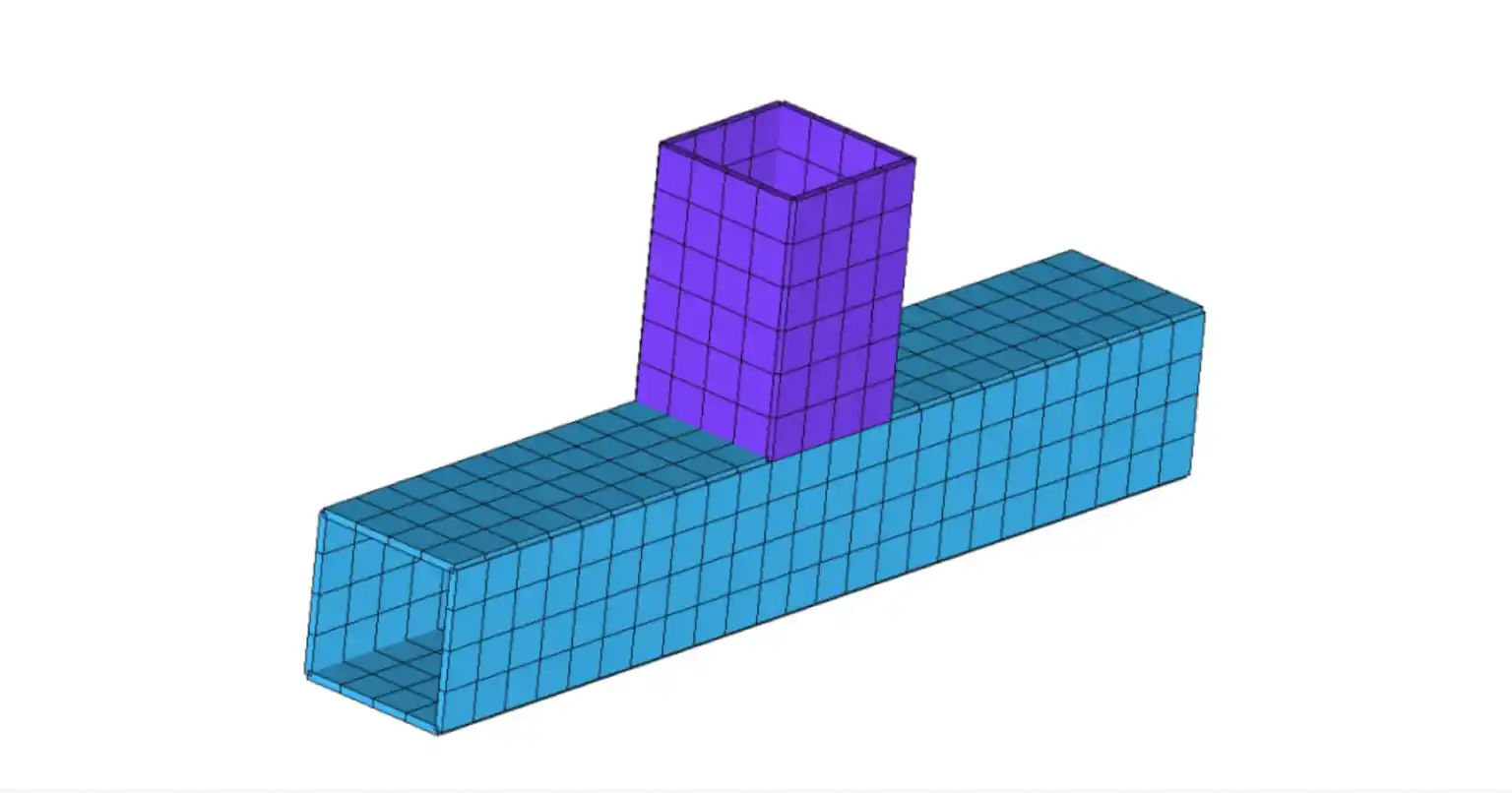
4. Integration with Simulation Tools
Parametric geometry can integrate with finite element analysis (FEA) software, enabling iterative testing and optimization, but the process is complex and often requires intermediate steps.
Updating parametric geometry affects the underlying FEA model, necessitating adjustments to the mesh to ensure compatibility. These updates sometimes result in the creation of additional models to accommodate changes in geometry, which complicates the workflow.
Image: FEA plate model of T-Joint connection, source
Benefits of Using Parametric Geometry in Structural Design
Using parametric geometry in structural design offers numerous benefits that enhance engineering projects’ efficiency, creativity, and performance. Here’s a detailed look at these advantages:
1. Design Flexibility
Parametric geometry allows for easy adjustments and modifications to the design by changing parameters. This flexibility helps explore various design alternatives quickly and efficiently without starting from scratch.
2. Improved Efficiency
By automating repetitive tasks and calculations, parametric design significantly reduces the time and effort required for manual modifications. This leads to faster project turnaround times and increased productivity.
3. Enhanced Optimization
Engineers can optimize designs for performance, cost, and material usage by systematically varying parameters. This approach helps identify the best solutions that meet specific design criteria and constraints.
5. Handling Complexity
Using parametric models, engineers can visualize and manage all dimensions and relationships in a single framework, reducing the likelihood of errors. This comprehensive approach allows for greater precision and consistency, as changes to one parameter automatically update the entire model, ensuring alignment and accuracy throughout the design process.
6. Real-time Interaction
Parametric design tools allow for real-time interaction with the model. Engineers can instantly see the effects of parameter changes, which helps them fine-tune the design and make informed adjustments on the fly.
7. Customization
Parametric geometry is ideal for projects requiring bespoke or unique structural elements. Engineers can tailor the design to specific needs and constraints, ensuring precision and consistency across the project.
8. Sustainability
Optimizing designs with parametric geometry can lead to more sustainable construction practices.
9. Cost-effectiveness
Parametric geometry can lead to cost savings in both the design and construction phases by enabling efficient design processes and optimization. For example, it can minimize material waste by optimizing structural layouts and reducing design time through automated updates to interdependent parameters. Reduced material usage and streamlined workflows contribute to overall project cost-effectiveness.
10. Innovation and Creativity
Parametric geometry fosters innovation by allowing engineers to explore unconventional shapes and forms, such as organic architectural structures like stadium roofs, pavilions, or biomimetic designs inspired by nature. While such complex shapes can also be created through traditional methods, parametric modeling streamlines the process by allowing quick modifications and real-time visualization of all dimensions and relationships.
Conclusion
Parametric geometry has become a cornerstone of modern structural design and optimization, providing engineers with tools for greater efficiency, adaptability, and precision. Its ability to facilitate iterative design, accommodate evolving project requirements, and integrate with advanced simulation tools allows for creating innovative and sustainable structures.
By reducing errors and enabling precise control over complex geometry, parametric geometry is set to remain a crucial component in addressing the growing demand for optimized, high-performance designs in structural engineering.