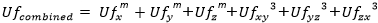Eurocode3 Fatigue (EN1993-1-9, 2005)
Eurocode3 Fatigue (EN1993-1-9, 2005) - a fatigue check according to the Eurocode 3: Design of steel structures - Part 1-9: Fatigue (January 2006).
To add Eurocode 3 standard execute from the ribbon:
Press  to Set Standard Custom Settings
to Set Standard Custom Settings
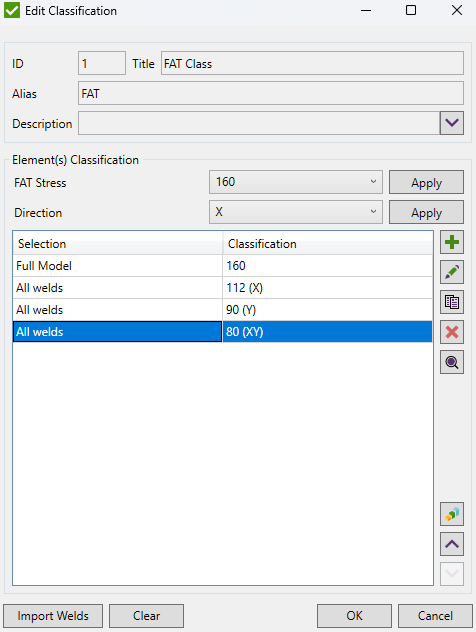
To perform the fatigue check FAT Class, Reduced Range, Consequence of Failure and Assessment Methods should be defined.
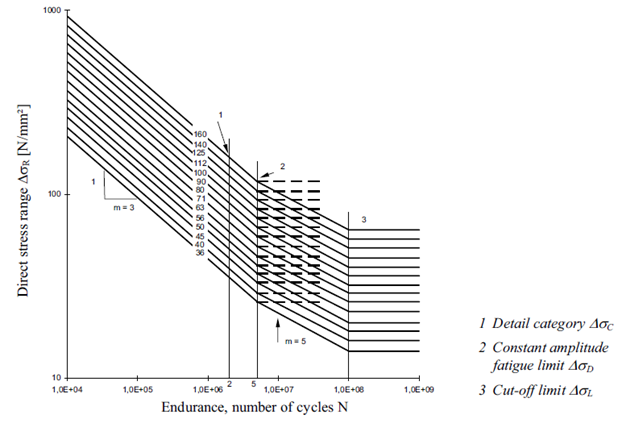
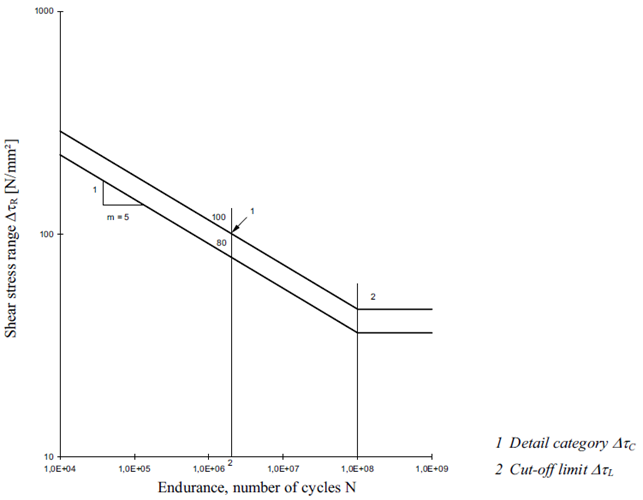
FAT Class - the fatigue strength for nominal stress ranges is represented by a series of 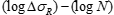 curves and
curves and 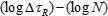 curves (S-N-curves), which correspond to typical detail categories. Each detail category is designated by a number which represents, in N/mm2, the reference value
curves (S-N-curves), which correspond to typical detail categories. Each detail category is designated by a number which represents, in N/mm2, the reference value  and
and  for the fatigue strength at 2 million cycles.
for the fatigue strength at 2 million cycles.
Fatigue strength curves for the direct stress ranges:
Fatigue strength curves for the shear stress ranges:
Press  to set the Weld Type (FAT Class).
to set the Weld Type (FAT Class).
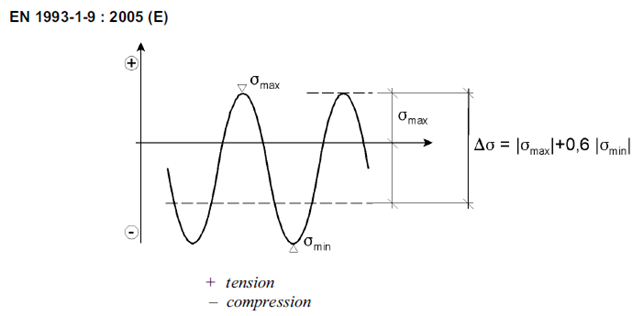
In non-welded details or stress-relieved welded details the effective stress range may be calculated by adding the tensile portion of the stress range and 60% of the magnitude of the compressive portion of the stress range:
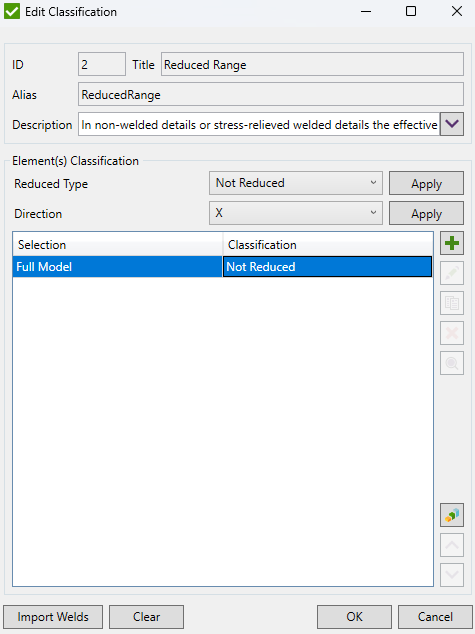
By default, delta stress is set to Not Reduced. Press  to specify the selection which should use reduced stress range:
to specify the selection which should use reduced stress range:
Safety factor Gamma_Mf depends on the Assessment method and the Consequence of failure:
| Assessment method | Consequence of failure | |
| Low consequence | High consequence | |
| Damage tolerant | 1,00 | 1.15 |
| Safe life | 1.15 | 1.35 |
The unit system is used for conversion units in check calculations. Conversion is used in Fatigue Strength at 2 million cycles calculations:
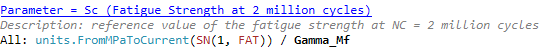
Standard uses material data (Yield/Tensile) in calculations. Wizard checks if the values are defined for all materials.
Use Hot Spot Stress - use Hot Spot Stress results for locations defined in Weld Finder Tool or Weld Stress results in the fatigue checks.
Include Rainflow Counting - include rainflow fatigue summation check with defined result category and method from which Rainflow Counting data will be used.
Note: category options for fatigue are Weld Stress or Hot Spot Stress.
Note: this option is available only for Enterprise licensing.
Calculation approach
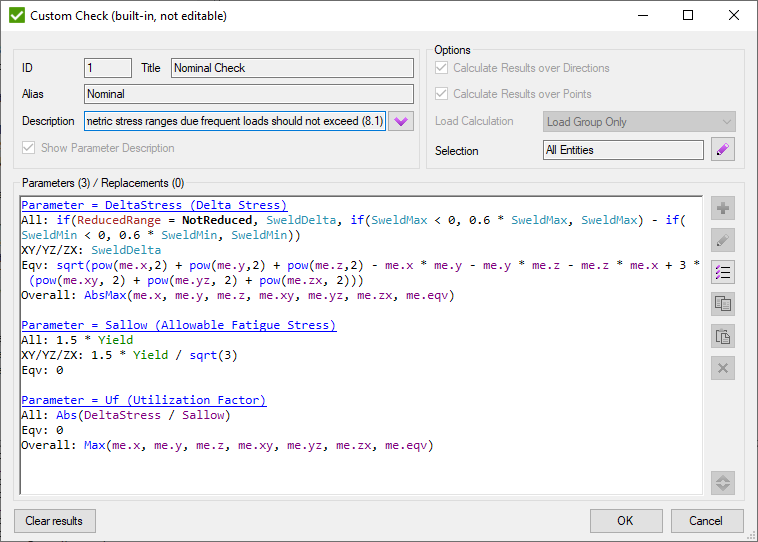
To verify a model according to the Eurocode3 fatigue 2 checks should be performed: Nominal Check and Fatigue Check.
The Nominal Check requires to verify if delta stress ranges are below the following limits:

The Fatigue Check is more complex than the Nominal Check. It requires to take into account the stress history (the stress ranges and their number of cycles). For this purpose Fatigue Group and Fatigue Summation Check were implemented in SDC Verifier.
Fatigue Group allows to take into account the stress history. Fatigue Summation Check runs the calculation for every Fatigue Group item (Load Group) and in the end makes a summation of fatigue damage (≤1).
Fatigue check requires to verify 2 conditions.
For normal and shear directions:
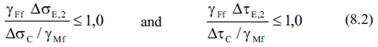
And combination rule:
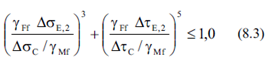
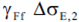 - delta stress range with partial factor;
- delta stress range with partial factor;
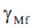 - safety factor.
- safety factor.
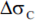 - allowable stress range. For some details from tables 8.1 to 8.10, depending on the wall thickness,
a Size Effect (kS) should be applied:
- allowable stress range. For some details from tables 8.1 to 8.10, depending on the wall thickness,
a Size Effect (kS) should be applied:
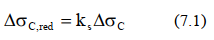
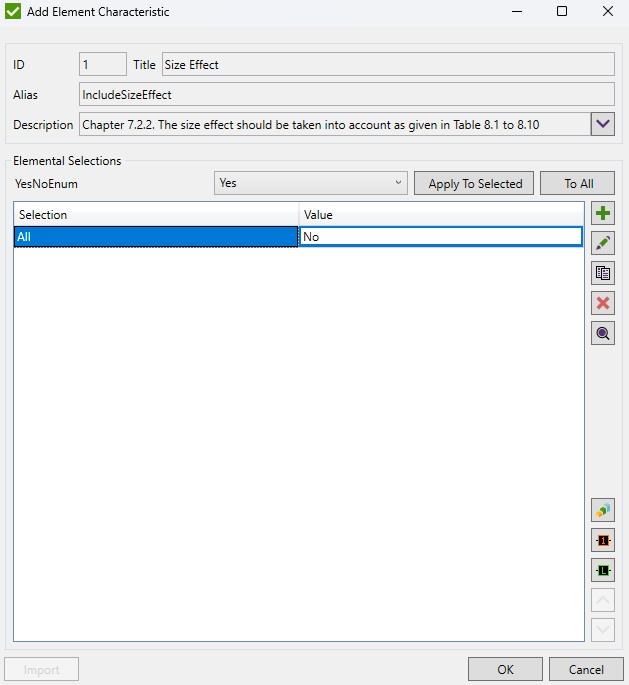
Details for which Size Effect should be applied can be set in elemental characteristic:
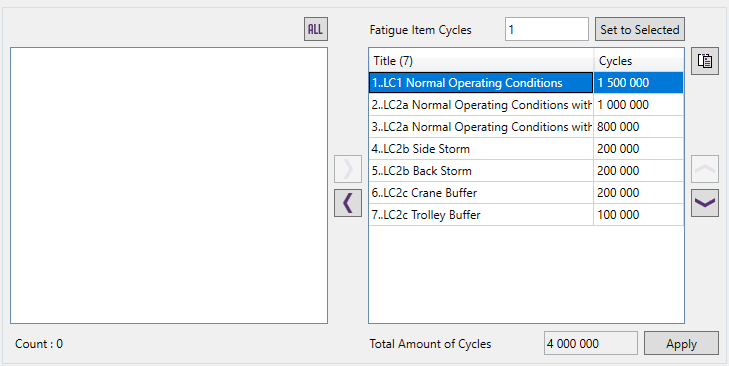
Example: Fatigue Group with a total amount of 4 million cycles:
Calculation procedure:
- Calculate Effective delta stress range.
- Calculates Fatigue damage for each Load Group based on stress range, fatigue strength and item amount of cycles
-
Perform summation of fatigue damage for items (Load Groups):
Summed Damage =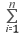 Fatigue Damage.
Fatigue Damage.
- Calculate Equivalent Damage (8.3):
- Overall Fatigue Damage. If overall fatigue damage < 1.0 then fatigue check is OK:
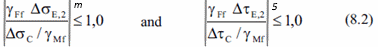
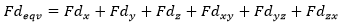
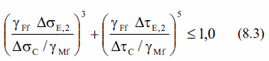
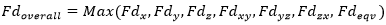
Damage root3 and Damage root5 should be used to evaluate an approximate overshoot for the damage.
The check "Fatigue Stresses Overshoots" should be used to estimate stress overshoots. The Allowable Stress is calculated for the Load Groups only using the stress history and the FAT class:
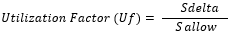
And the combination rule: