Norsok N004 (Rev. 3, 2013)
Norsok N004 (Rev. 3, February 2013) Standard - specifies structural strength and stability requirements for steel tubular members.
This standard is applied to the cylindrical members with Thickness ≥ 6mm, ratio D / t < 120 and Yield < 500 MPa.
To add the standard execute from the ribbon:
Press  to Set Standard Custom Settings
to Set Standard Custom Settings
Safety Factors are set to Standard default values. It is not necessary to change them. Material Safety Factor is calculated according to the section 6.3.7 by default but it is possible to set a constant value.
According to the calculation procedure, Beam Length for Y and Z direction is required. Data from Beam Member Finder is used automatically.
If beam members are not recognized press  .
.
Standard uses material data (Yield/Tensile) in calculations. Wizard checks if the values are defined for all materials.
It is possible to use Norsok N004 (Rev. 3, 2013) in combination with AISC 360-10 Members (14th, 2010) or
Eurocode3 Members (EN1993-1-1, 2005).
Set option Calculate Non-Tubular Shapes According To: checked and pick the standard for non-tubular elements.
Press  to define settings.
to define settings.
Note: If the AISC 360-10 or Eurocode3 is included - 3 standards will be created:
- Norsok N004 - circular tubes are calculated according to Norsok N004;
- AISC 360-10 / Eurocode3 - all supported shapes are calculated according to AISC 360-10 / Eurocode3;
- AISC/Eurocode3 and Norsok - combined standard where results for circular tubes are taken from Norsok N004 and results for other supported shapes - according to AISC 360-10 / Eurocode3.
Joint Check
Joint Check is a part of the Norsok N004 standard but is available for Custom Standard. To create a new Joint Check execute from the checks context menu of a respective standard.
Press  to automatically highlight single Connection selected in the table.
to automatically highlight single Connection selected in the table.
Recognition Settings are described in Common Options chapter.
Set Connection ID and press to display connection in the table.
Joint check is based on connections. Each connection is a set of elements near joint node (see Joints Finder). Connections consists of Chord and braces. Brace contains only 1 element with ID defined in brackets (#). Connection can contain braces from the both sides of the chord. Information is displayed in second brackets: U- upper braces; L- lower braces;
Press to find all connections of the model. Window with connections that are recommended to be checked manually will be displayed:
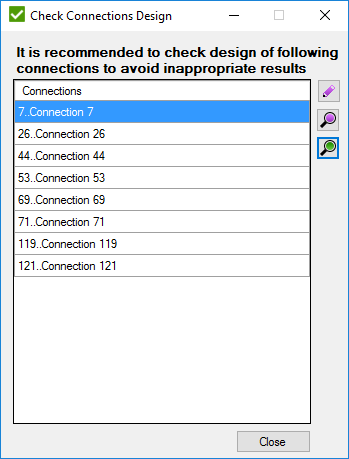
Connection has to be checked when:
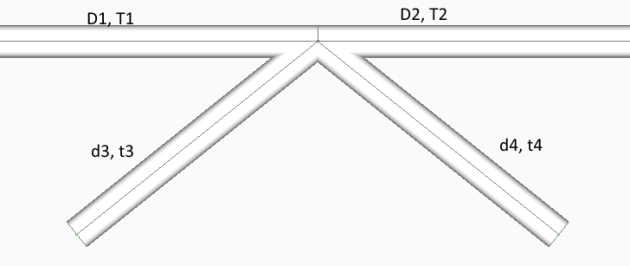
- D1 = D2 = d3 = d4, T1 = T2 = t3 = t4
- D1 = D2 = d4, T1 = T2 = t4, d3 > D1
- D1 = D2 = d3 = d4, T1 = T2 = t4, t3 > T1 according to the following image
 - Add new connection manually:
- Add new connection manually:
 - edit selected connection;
- edit selected connection;
 - preview highlight selected connection;
- preview highlight selected connection;
 - preview only selected connection;
- preview only selected connection;
 - remove selected connection;
- remove selected connection;
 - plot all connections values in colors + Labels with IDs;
- plot all connections values in colors + Labels with IDs;
 - show information about all connections;
- show information about all connections;
 - hide information of all connections.
- hide information of all connections.
 - clear all calculations for loads;
- clear all calculations for loads;
Edit Connection
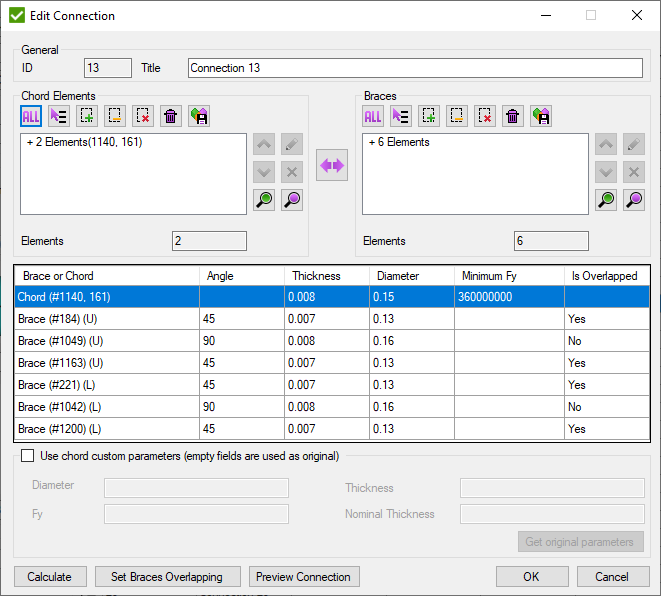
Pick Chord elements and braces (each brace consist of 1 element) and press to preview connection properties.
 - swap chord and brace selections
- swap chord and brace selections
Press to highlight connection on the model.
- open window to set the overlapping brace. Is enabled only if one brace overlaps another one in connection:
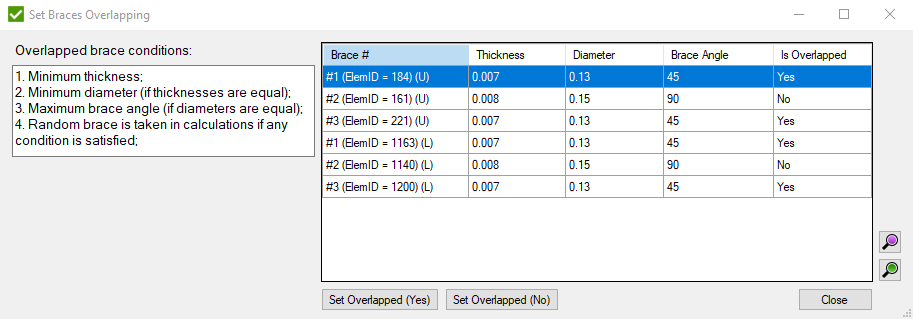
- set to the selected braces if they are overlapped.
 - set if use can calculations (section 6.4.3.5) and effective length:
- set if use can calculations (section 6.4.3.5) and effective length:
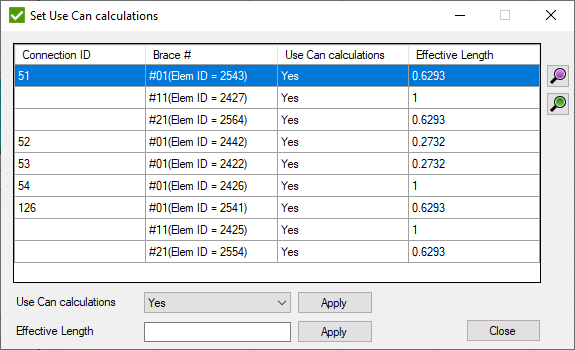
Select Use Can calculations and press to set if formula 6.56 will be applied to all selected braces.
Fill Effective Length and press to set the value to all selected braces.
Note: Effective Length is applied only to the braces that Use Can Calculations.
Joint Check Results
Mathematical background
All calculations are performed in accordance to Norsok N004 (Rev.3, Feb 2013).
Nomenclature and geometric parameters that are used in results:
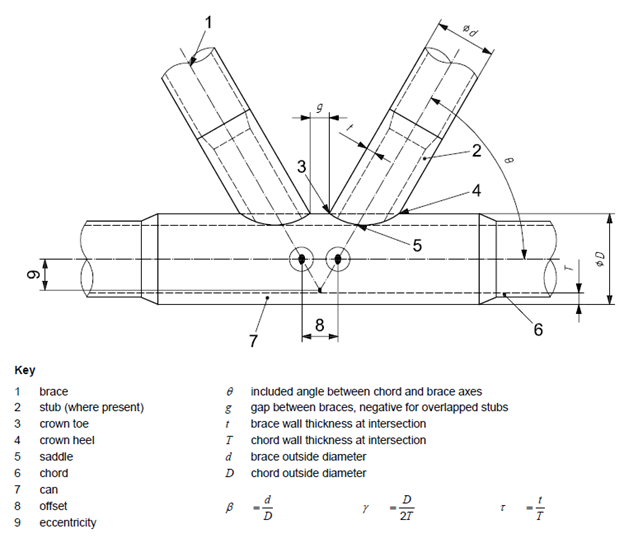
The validity ranges of connection parameters:
0.2 ≤ β ≤ 1.0
10 ≤ γ ≤ 50
30° ≤ θ ≤ 90°
g/D ≥ -0.6 (for K joints)
fy ≤ 500N/mm2
fy - chord allowable static stress = Min(yield stress, tensile strength * 0.8).
For each brace connected to the chord, connection elements of the chord are taken into account. The minimum allowable stress is taken if elements are of different materials.
Note: If material yield stress > 500 Mpa - allowable static stress is taken equal to material yield stress.
Brace Types. According to the standard, joint types are defined by following rules:
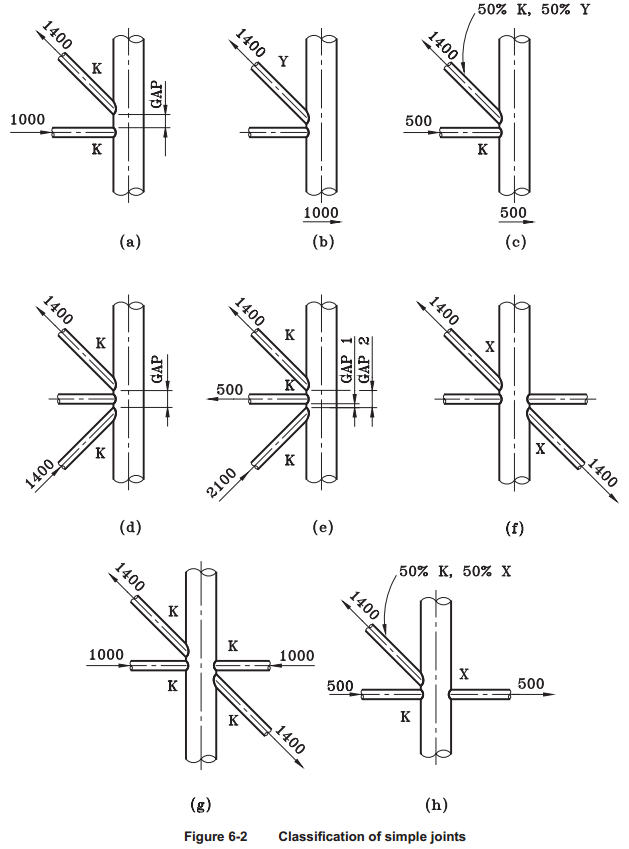
Joint type is based on type of loading. By checking if forces of connection are balanced joint types are classified on K, TY, and X (Cross).
K - tension and compression loads are balanced.
TY - tension or compression load goes as a shear force in a chord.
X (Cross) - Connection has to contain braces from the both sides to check on a cross joint. If balanced forces of all braces on one side and balanced forces of all braces of other side are equal then all braces are classified as X (Cross).
Interpolation - the order of joint type recognition is following: K -> X (Cross) -> TY. Each brace can have all 3 types of the joint type taken as a percentage of the axial load of a brace to a summation of all braces loads.
Note: If brace has 0 force joint type for such brace is set to TY.
Gap calculations. .The gap is a minimum distance between two differently loaded braces (tension and compression) measured on a shell of the chord.
Gaps depend on the Load and are calculated only between the braces with different axial forces (tension and compression). Otherwise the gap = 0.
Note: Overlapping braces can contain negative gap if they are loaded in a different way.
Note: It is possible that brace can have two or more gaps to considerate. a percentage of each gap is calculated using the forces of the connection.
Basic Joint Strength.
Joint axial and bending capacities shall satisfy the following equations:
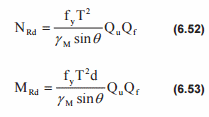
where
NRd - the joint design axial resistance;
MRd - the joint design bending moment resistance;
fy - the yield strength of the chord member at the joint;
ϒM = 1.15;
T - the chord wall thickness at the intersection with the brace;
d - the brace outside diameter;
θ - included angle between the brace and the chord;
Qu - the strength factor;
Qf - the chord force factor;
Strength factor Qu
Qu is the strength factor which varies with the joint and the action type:


where
fy,b - the yield strength of brace;
fy,c - the yield strength of chord;
t - the brace wall thickness;
For -0.05 ≤ g/D < 0.05, the gap factor Qg is calculated as linear interpolation between the limiting values of the above expressions:
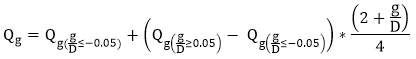
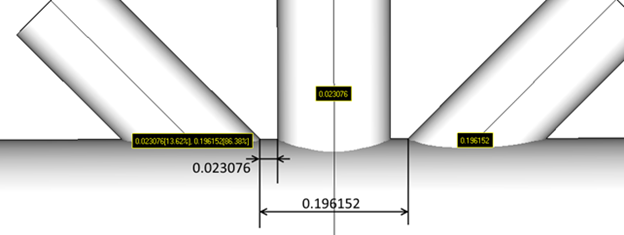
Note: g - the total gap of the brace. From the following picture g = 0.023076 * 0.1362 + 0.196152 * 0.8638 = 0.172579;
Chord force factor Qf
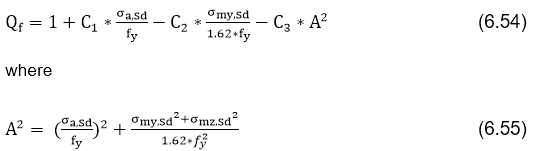
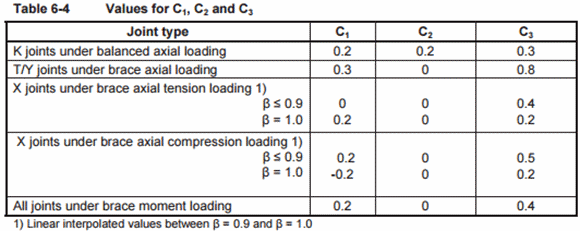
σa,Sd - the design axial stress in chord, positive in tension;
σmy,Sd - the design in-plane bending stress in chord, positive for compression;
fy - the - yield strength;
C1,C2,C3 - the coefficients depending on the joint and the load type:
The average of the chord loads and bending moments on either side of the brace intersection should be used in the formulas (6.54), (6.55). The chord thickness at the joint should be used in the above calculations.
Qf total = QfK * brace percentage K + QfTY + brace percentage TY + QfX * brace percentage X -for the axial loading;
Extra joint axial capacity calculations are performed to the connections that contain increased thickness of the chord. The axial strength is calculated by following formula:
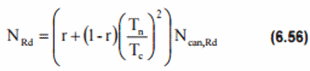
where
Ncan,RD - NRD from the equation (6.52) based on the chord can geometric and material properties including Q_f calculated with respect to the chord can;
Tn - the nominal chord member thickness;
Tc - the chord can thickness;
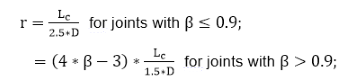
Note: r cannot be taken greater than 1;
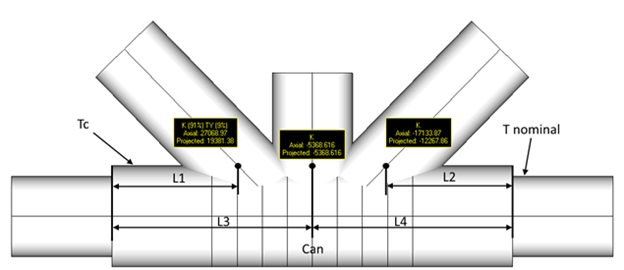
Effective length L is calculated for each brace separately. It is a minimum distance from the end of can till the point of intersection of chord and brace multiplied on 2.
Tc ≥ T nominal;
L1,L2 ≤ 1.25 * D. If L1 and L2 and L2 exceed 1.25 * D distance, can will not be recognized;
D - the can diameter;
L = 2 * L1 - the effective length for the left brace;
L = 2 * L3 = 2 * L4 - the effective length for the middle brace;
L = 2 * L2 - the effective length for the right brace.
Note: This section is applied to the connections with cans. If the brace Lc 0 section is not applied. If the brace is overlapping the section is not applied.
Strength check
Joint resistance shall satisfy following interaction equation for axial force and/or bending moments in the brace:
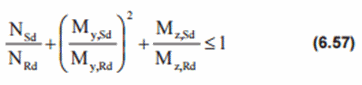
for all joints, except those, that identified as non-critical
where
NSd - the design axial force in the brace member;
NRd - the joint design axial resistance;
My,Sd - the - design in-plane bending moment in the brace member;
Mz,Sd - the design out-of-plane bending moment in the brace member;
My,Rd - the design in-plane bending resistance;
Mz,Rd - the design out-of-plane bending resistance;
Overlapping joints
The strength of the joints that have in-plane overlap involving two or more braces may be determined using the requirements for simple joints defined in 14.3, with the following exceptions and additions.
a) Shearing of the brace parallel to the chord face is a potential failure mode and shall be checked.
Shear capacity = fy * effective area /√3 - 1.05)
Effective area is the total area of two braces that overlap:
Area1 = 2 * p1* t1 - the area of the through brace;
Area2 = 2*(p2-q) * t2 - the area of the overlapping brace;
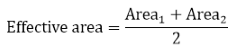
where
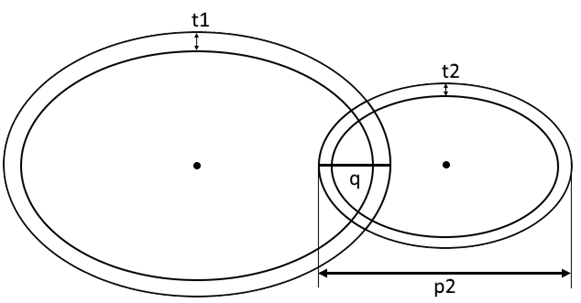
t1 - the thickness of the through brace;
t2 - the thickness of the overlapping brace;
p1 = d1/sin(θ1);
p2 = d2/sin(θ2);
d1, d1 - the original diameter of the through and overlapping braces respectively;
θ1, θ2 - the inclination of the through and overlapping braces respectively to the chord;
q - the overlapping distance (negative gap);
Applied shear force is taken as the summation of forces, perpendicular to the chord of the through and the overlapping braces;
Shear UC (Ultimate Capacity) is calculated as the relation of Applied shear force to shear capacity:
Shear UC = Applied shear force / Shear capacity
b) Section 6.4.3.5 (can calculations) does not apply to overlapping joints.
c) If axial forces in the overlapping and through braces have the same sign, the combined axial force representing that in the through brace plus a portion of the overlapping brace forces should be used to check the through brace intersection capacity. The portion of the overlapping brace force can be calculated as ratio of cross sectional area of the brace that bears onto the through brace to the full area.
Modified axial force= Pd1+Pd2 * ov;
where
Pd1 - the axial force of the through brace perpendicular to the chord.
Pd2 - the axial force of the overlapping brace perpendicular to the chord.
ov - overlapping percentage,
ov=q/p*100%;
Modified axial UC= Modified axial force / NRd;
NRd - the joint axial capacity from the formula (6.52);
d) For both in-plane or out-of-plane moments, the combined moments on the overlapping and through braces shall be used to check the through brace intersection capacity. This combined moment shall account for the sign of the moments.
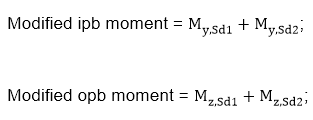
My,Sd1, My,Sd2, Mz,Sd1, Mz,Sd2 - the respective in-plane and out-of-plane bending moments of the through and overlapping brace;
Modified moment UC= (Modified ipb moment / My,Rd)2+Modified opb moment / Mz,Rd
Modified axial and moment UC=Modified axial UC+Modified moment UC
Particular cases
Sometimes models cannot represent real situations. For such cases calculations are updated to get the worst possible result according to the parameters:
Case1:
Sometimes models cannot represent real situations. For such cases calculations are updated to get the worst possible result according to the parameters:
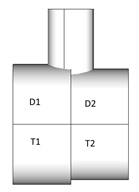
When Chord is formed by elements with different properties around the joint node and D1<>D2, D = min(D1, D2); T = min(T1, T2) are considered for calculations.
Case 2:
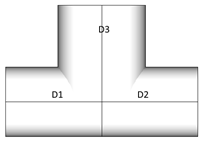
D1=D2, D1<D3. For such case D3 is recognized as chord as it has bigger diameter. Naturally pipe of bigger diameter cannot be welded to smaller. Such connections are recommended to be checked.
Case 3:
a)
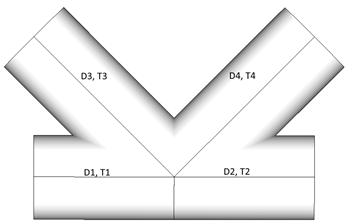
D1 = D2 = D3 = D4;
T1 = T2 = T3; T4 >T4;
When all diameters of connection are equal, thicknesses are compared. Element with thickness = T4 is recognized as chord.
b) In case when:
D1 = D2 = D3 = D4;
T1 = T2 = T3 = T4;
When all elements of connection are of the same dimensions, chord is recognized as pair of elements that form straight line. If any pair that matches conditions is found, random element will be recognized as a chord.
